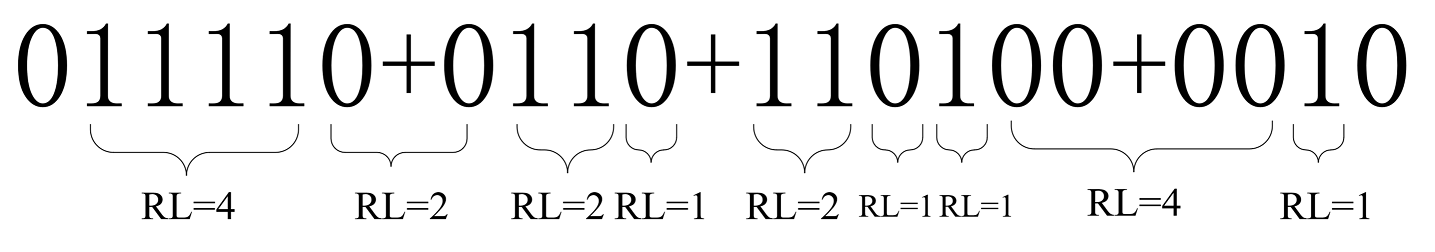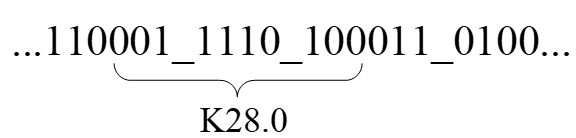背景

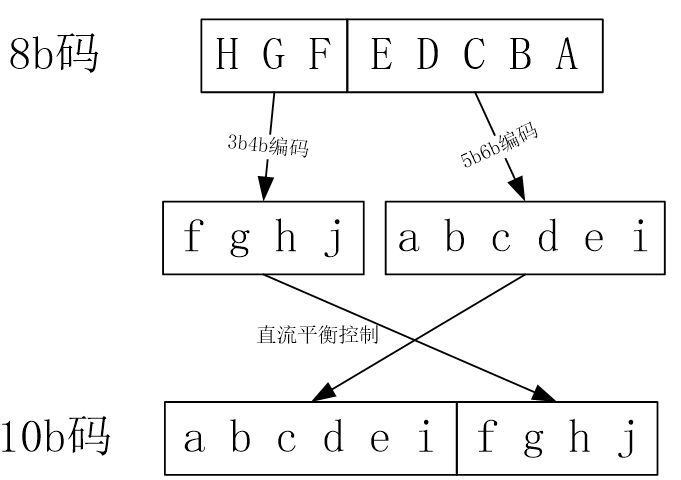
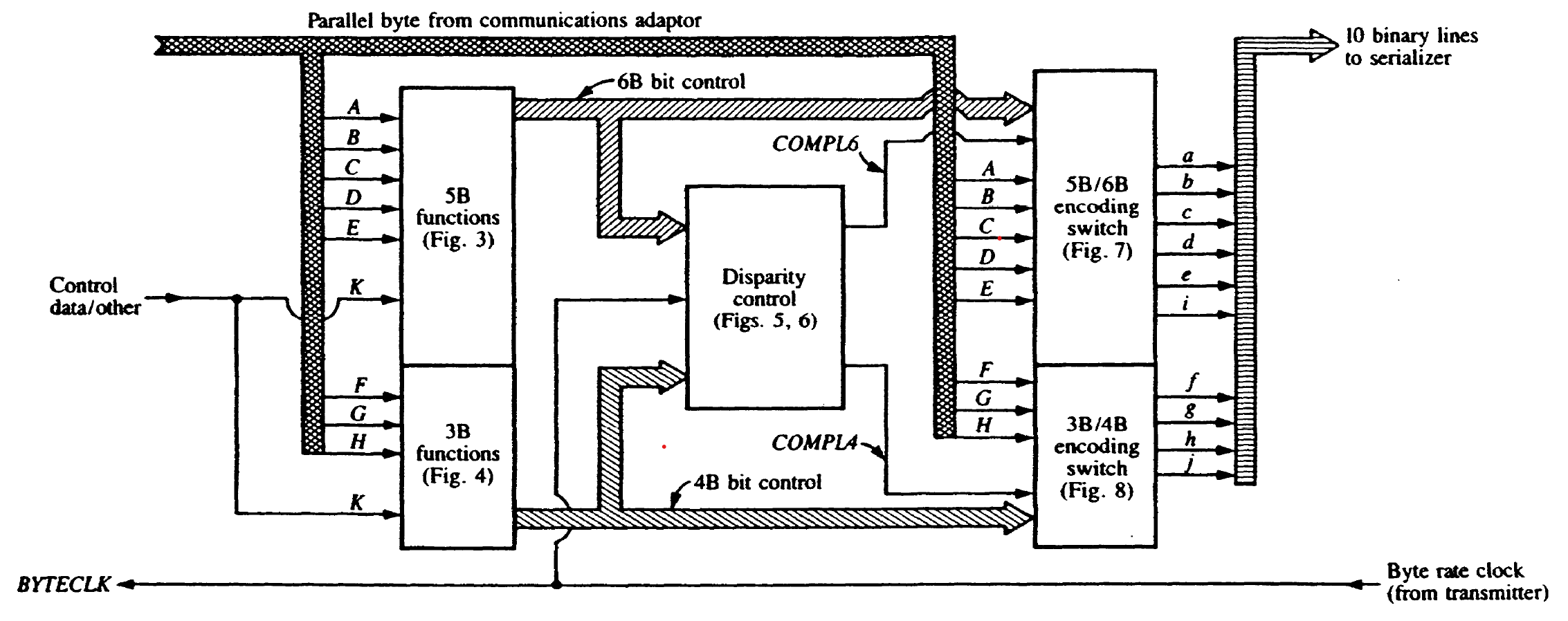
关于为什么要进行8b10b编码，主要是为了直流平衡（dc balance），由于交流耦合会导致信号抖动、ISI等问题。可以参考8B/10B编码基本原理。
本文基于1983年IBM的8b10b编解码的原文章A DC-Balanced, Partitioned-Block, 8B/10B Transmission Code | IBM Journals & Magazine | IEEE Xplore。
8b10b编码分为5b6b和3b4b两个部分，其编码逻辑如下图所示：

8b10b_enc

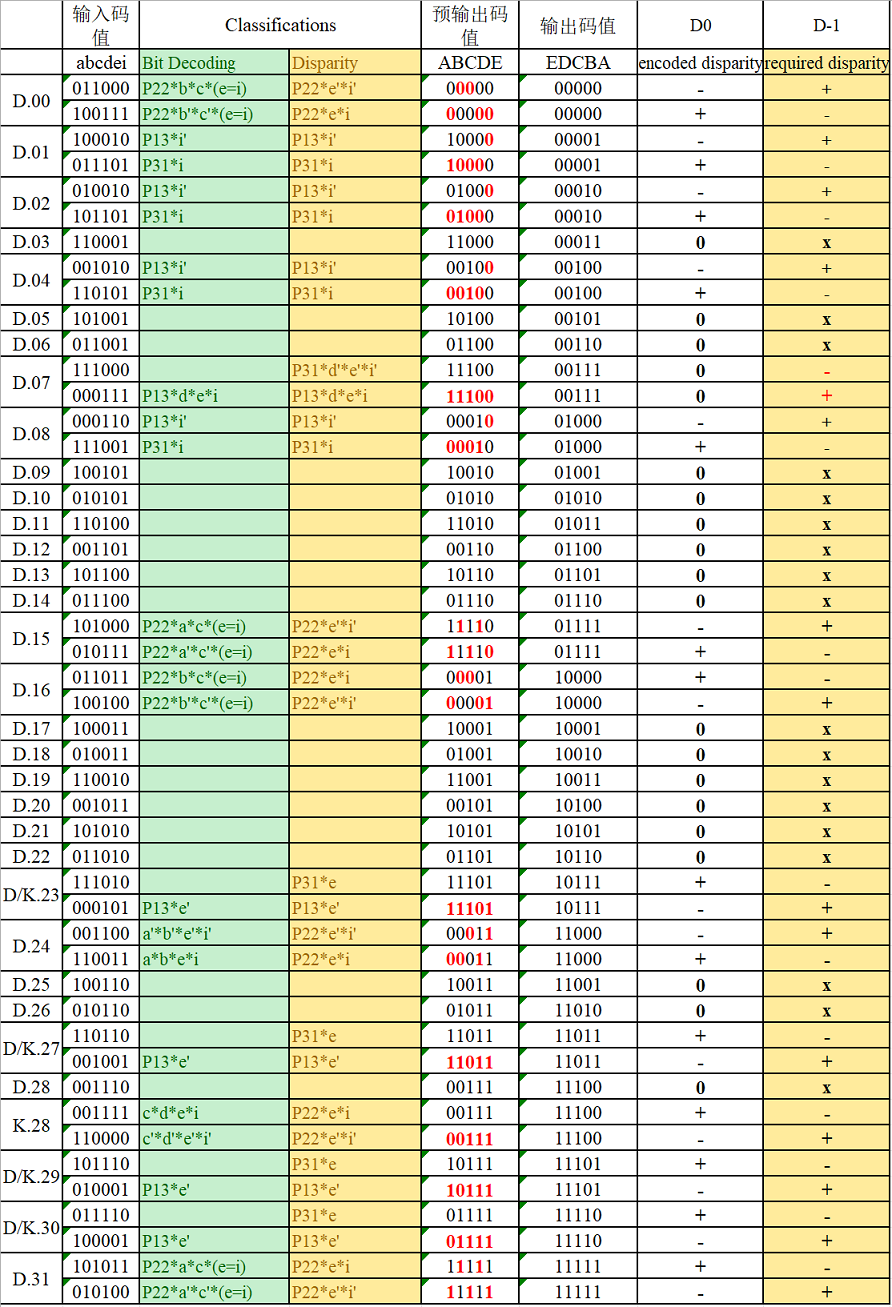
一般材料会采用5b6b和3b4b如下的两个编码表，但却没有说明EDCBA到abcdei的命名方式，以及原本编码的具体逻辑。

5b6b_enc

3b4b_enc

原理分析

数据码

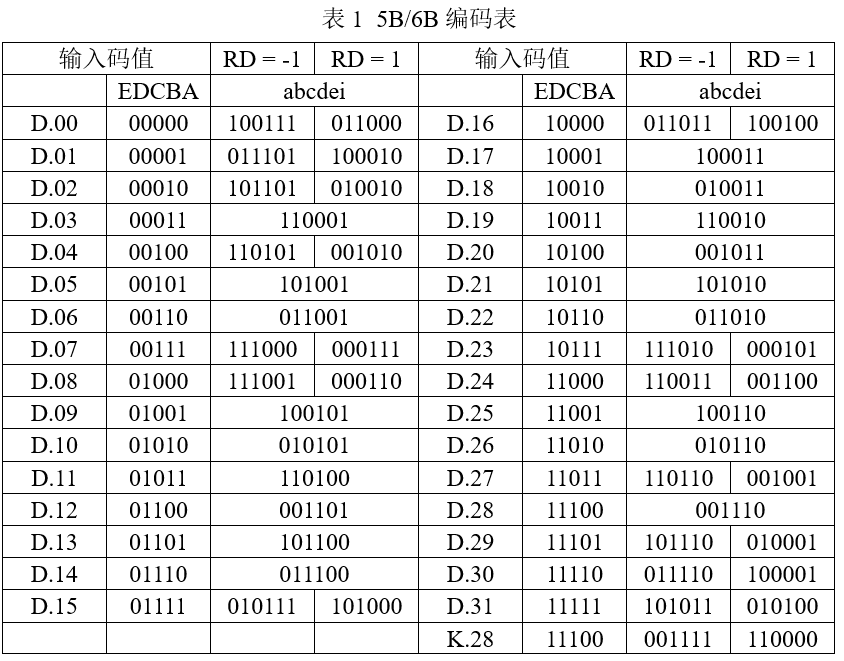
5b6b

5b6b_d

D.x.y中的.x代表8b数据中5b的部分，比如D.13.y就是5'b01101。

5b6b的编码逻辑：

将5b数据EDCBA倒为ABCDE，最后一位I统一补0，形成ABCDEI
观察ABCDEI的0，1数量是否平衡，
- 0，1平衡（各3个），直接输出abcdei=ABCDEI
- 0，1不平衡，根据码表进行比特位翻转
  - 码表无标红比特位，直接输出abcdei=ABCDEI
  - 码表有标红比特位，翻转对应比特位

举例：

D.11.y：EDCBA=01011，倒转补0后ABCDEI=110100，0，1平衡，不需要翻转码字，abcdei=ABCDEI=110100
D.18.y：EDCBA=10010，倒转补0后ABCDEI=010010，0，1不平衡，根据码表翻转码字I，abcdei=ABCDEI'=010011
D.24.y：EDCBA=11000，倒转补0后ABCDEI=000110，0，1不平衡，根据码表翻转码字C和E，abcdei=ABC'DE'I=001100
D.30.y：EDCBA=11110，倒转补0后ABCDEI=011110，0，1不平衡，根据码表，不需要翻转码字，abcdei=ABCDEI=011110
D.31.y：EDCBA=11111，倒转补0后ABCDEI=111110，0，1不平衡，根据码表翻转码字B、D和I，abcdei=AB'CD'EI'=101011

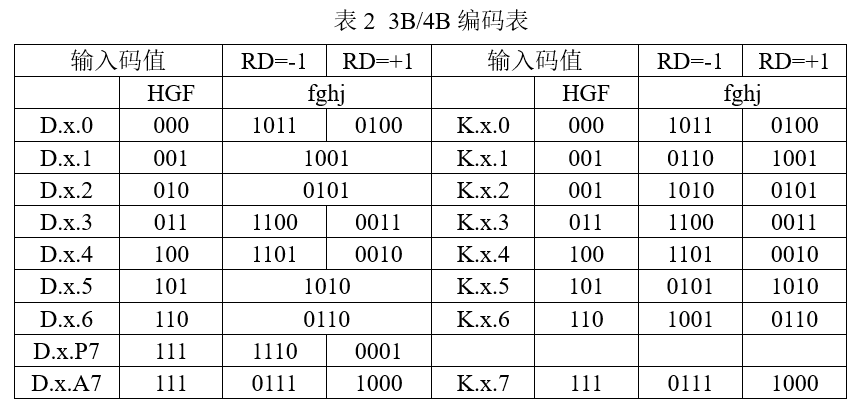
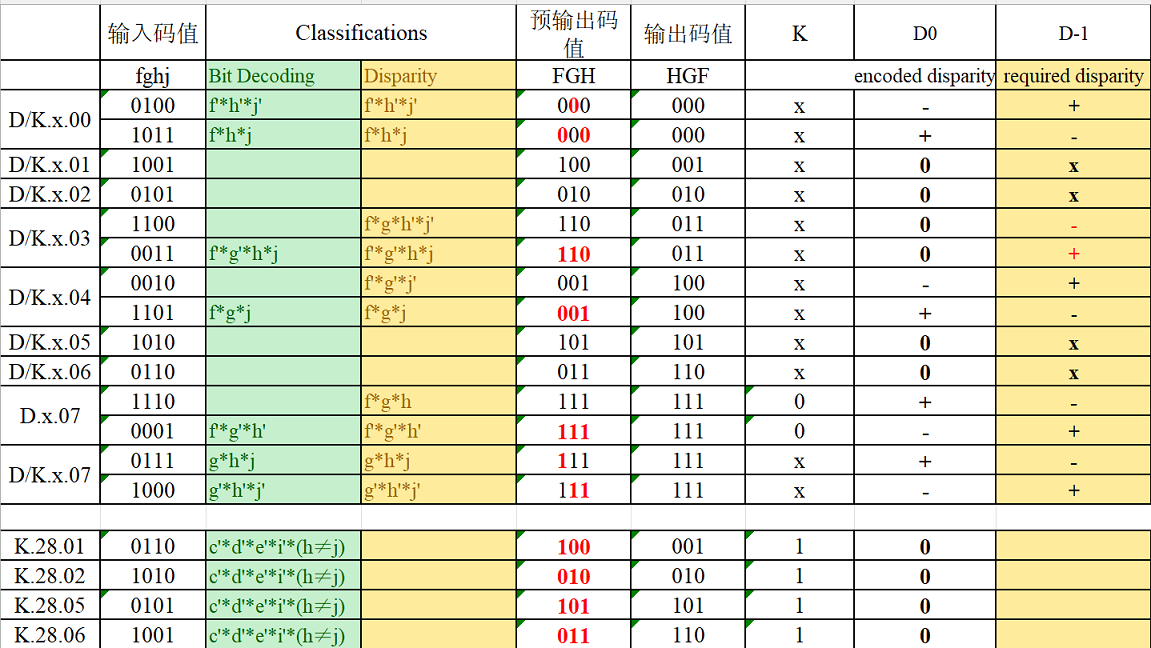
3b4b

3b4b_d

D.x.y代表中的.y代表8b数据中3b的部分，比如D.x.4就是3'b100。

3b4b的编码逻辑：

将3b数据HGF倒为FGH，最后一位J统一补0，形成FGHJ
观察FGHJ的0，1数量是否平衡，
- 0，1平衡（各2个），直接输出fghj=FGHJ
- 0，1不平衡，根据码表进行比特位翻转
  - 码表无标红比特位，直接输出fghj=FGHJ
  - 码表有标红比特位，翻转对应比特位

举例：

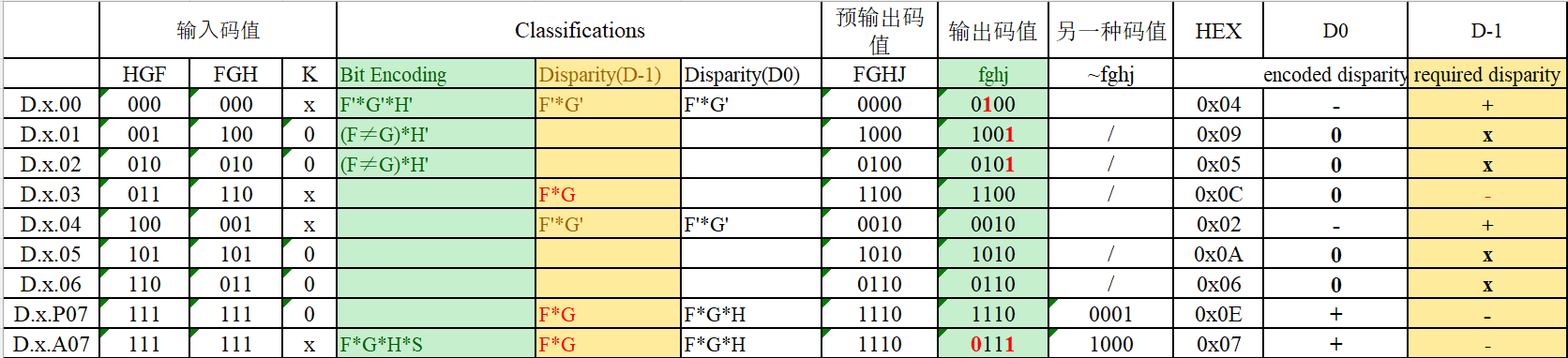
D.x.3：HGF=011，翻转补0后FGHJ=1100，0，1平衡，不需要翻转码字，fghj=FGHJ=1100
D.x.1：HGF=001，翻转补0后FGHJ=1000，0，1不平衡，根据码表翻转码字J，fghj=FGHJ'=1001
D.x.4：HGF=100，翻转补0后FGHJ=0010，0，1不平衡，根据码表，不需要翻转码字，fghj=FGHJ=0010
D.x.7：
- D.x.P07：HGF=111，翻转补0后FGHJ=1110，0，1不平衡，根据码表，不需要翻转码字，fghj=FGHJ=1110
- 若D.x.P07有码流不平衡风险，则使用D.x.A07（Alternative，备用码）根据码表翻转码字F和J，fghj=F'GHJ'=0111
- 关于D.x.P07和D.x.A07，后续章节会详细讲解。

数据极性

不论是5b6b编码，还是3b4b编码，其编码均有属性叫做极性（disparity），极性代表这个码字0和1的数量多少。

5b6b举例：

D.24.y，其6b编码为001100，0比1的数量多2，其极性为-，实际为-2
D.30.y：其6b编码为011110，1比0的数量多2，其极性为+，实际为+2
D.11.y：其6b编码为110100，1和0的数量一样，其极性为空，实际为0

3b4b举例：

D.x.0：其4b编码为0100，0比1的数量多2，其极性为-，实际为-2
D.x.7：其4b编码为1110或0111，1比0的数量多2，其极性为+，实际为+2
D.x.6：其4b编码为0110，1和0的数量一样，其极性为空，实际为0

观察5b6b和3b4b的编码表可以发现，输出的6b编码和4b编码只存在两种形式：

极性码
- 0和1的数量不平衡的码字，编码表中不平衡数量仅为2，因此极性码的极性为±2
- 001100(+2)，011110(-2)等是6b极性码
- 0100(+2)，1110(-2)等是4b极性码
平衡码
- 0和1的数量平衡的码字，平衡码的极性为0
- 110100，101001等是6b平衡码
- 0110，0101等是4b平衡码

极性码

极性码按照码表编码，但最终输出的码字有两种。

直接编码出来原始的码字
直接编码后按位取反的码字

举例：

D.24.y，原始6b编码为001100，其极性为-，另一种码字为110011，其极性为+
D.30.y：原始6b编码为011110，其极性为+，另一种码字为100001，其极性为-
D.x.0：原始4b编码为0100，其极性为-，另一种码字为1011，其极性为+
D.x.7：原始4b编码为1110，其极性为+，另一种码字为0001，其极性为-

极性码是±极性（positive/negative disparity）的。

平衡码

虽然平衡码都是0和1的数量平衡的码，但他们码字中0和1的间隔不一定一致，可简单分为两种。

完美平衡码（Perfect Balance Code）
- 6b编码：010101，010101，101100等
- 4b编码：0101，1001等
不完美平衡码（Imperfect Balance Code）
- 6b编码：111000
- 4b编码：1100

平衡码是0极性/空极性（zero/null disparity）的。

特殊极性码

前面讨论过，D.x.7是一种特殊的极性码，他有两种原始码字。

D.x.P07：原始4b编码为1110，其极性为+，另一种码字为0001，其极性为-
D.x.A07：原始4b编码为0111，其极性为+，另一种码字为1000，其极性为-

这种特殊的极性码是为了码间的直流平衡设计的，关于D.x.P07和D.x.A07，可以参考示例2中的实际使用。

极性控制

运行极性

运行极性/运行不一致性（Running Disparity，RD），指的是在编码产生码流的过程中，实时的码流极性。

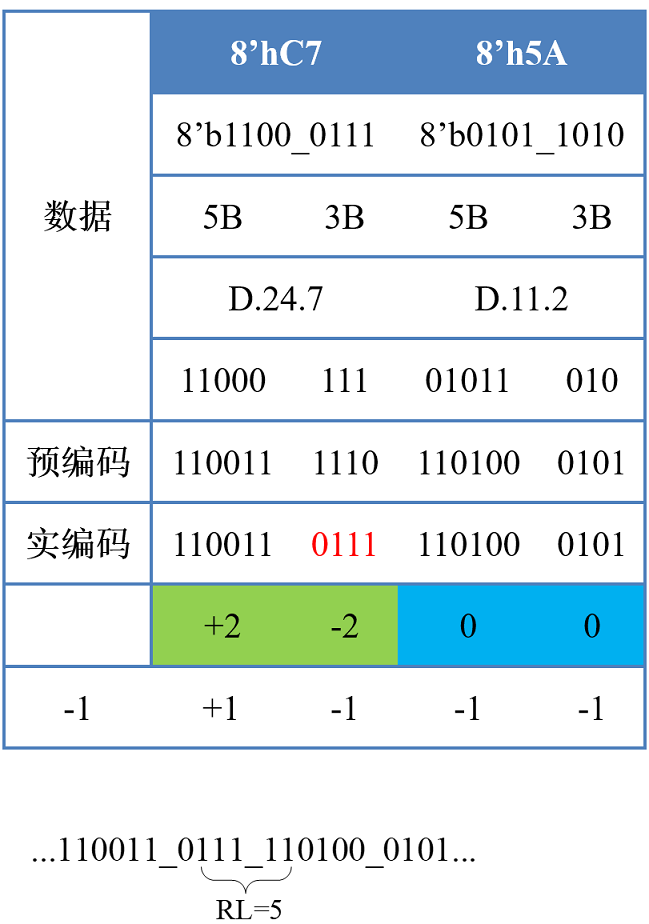
比如编码D.30.6+D.11.4的码流，运行极性（RD）分析如下：

编码过程：011110+0110+110100+0010
假设初始极性为-1，则运行极性（RD）：RD = -1 + 2 + 0 + 0 - 2 = -1

运行长度

运行长度（Running Length，RL），指的是连续0或者1的数量，注意运行长度不止代表码字内的连续0,1数量，也代表码字间的连续0,1数量，是衡量整个数据流是否直流平衡的一种方式。

比如编码D.30.6+D.11.4的码流，运行长度（RL）分析如下：

编码过程：011110+0110+110100+0010

控制原则1

控制直流平衡，有两个方面的考虑：

-2<RD<2，运行极性不超过±2，即总体码流的0,1数量相同
RL<5，运行长度不超过5，即总体码流连续0,1数量不超过5

这里首先考虑RD的控制总体原则：

当前编码极性为空（0），则继承码流极性，当前编码不变
当前编码极性非空（±2），则保持码流极性平衡
- 若当前编码与码流极性相同，则按位取反，翻转极性
- 若当前编码与码流极性相反，则保持编码，保持极性

简单来说，就是0多了补1，1多了补0，0、1一样多则不变的意思。

示例1

假设发送码流8'h55,8'hC0,8'hF2,8'hF4，初始极性为RD=-1，编码极性简写为disp（disparity）

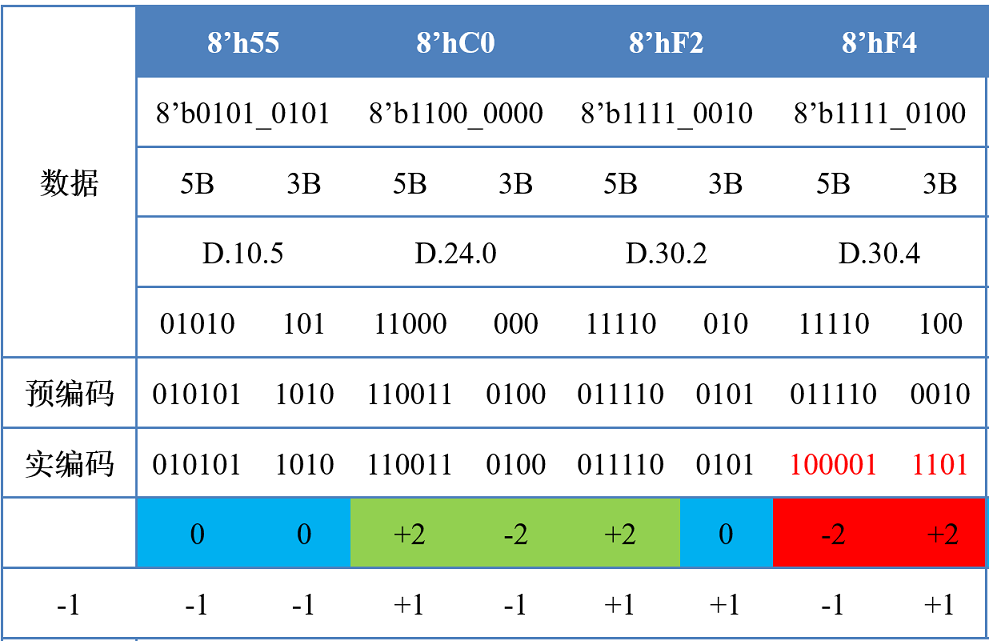
8'h55=8'b01010101
- 5B=5'b01010=5'd10，3B=3'b101=3'd5，D.10.5
- 5B编码：6B=6'b010101，disp=0，继承码流极性，RD=-1+0=-1
- 3B编码：4B=4'b1010，disp=0，继承码流极性，RD=-1+0=-1
8'hC0=8'b11000000
- 5B=5'b11000=5'd24，3B=3'b000=3'd0，D.24.0
- 5B编码：6B=6'b110011，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b0100，disp=-2，保持极性（当前码流RD=+1），RD=+1-2=-1
8'hF2=8'b11110010
- 5B=5'b11110=5'd30，3B=3'b010=3'd2，D.30.2
- 5B编码：6B=6'b011110，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b0101，disp=0，继承码流极性，RD=+1+0=+1
8'hF4=8'b11110100
- 5B=5'b11110=5'd30，3B=3'b100=3'd4，D.30.4
- 5B编码：6B=6'b011110，disp=+2，翻转极性（当前码流RD=+1），6B=6'b100001，disp=-2，RD=+1-2=-1
- 3B编码：4B=4'b0010，disp=-2，翻转极性（当前码流RD=-1），4B=4'b1101，disp=+2，RD=-1+2=+1

eg1

控制原则2

在控制原则1中，只讨论了RD控制，虽然正常的RD控制可保证RL<5，但一些特殊情况需要进行特殊控制。

不完美平衡码

不完美平衡码的定义参考平衡码。不完美平衡码也必须按极性码的做法保持码流极性平衡，保持或翻转编码。

6b不完美平衡码举例：

假设发送码流8'A8,8'h38，初始极性为RD=-1，编码极性简写为disp（disparity）

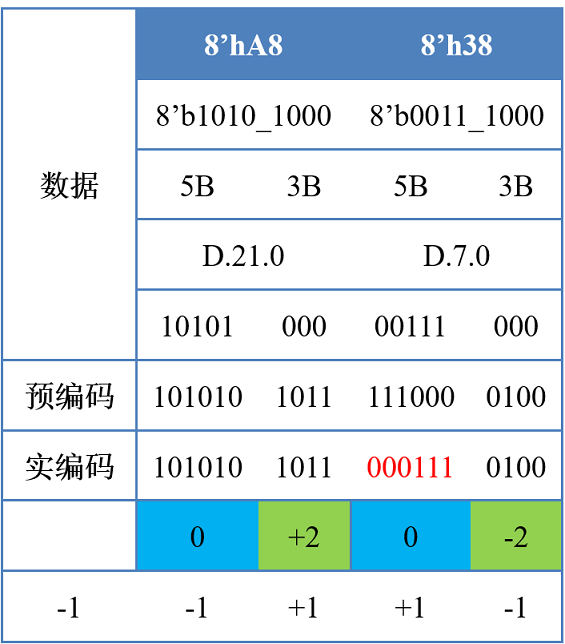
8'hA8=8'b10101000
- 5B=5'b10101=5'd21，3B=3'b000=3'd0，D.21.0
- 5B编码：6B=6'b101010，disp=0，继承码流极性，RD=-1+0=-1
- 3B编码：4B=4'b1011，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
8'h38=8'b00111000
- 5B=5'b00111=5'd7，3B=3'b000=3'd0，D.7.0
- 5B编码：6B=6'b111000，disp=0
  - 此时，如果按照disp=0，继承码流极性，当前编码不变的话，则前面4B的1011和6B的111000会形成1011_111000，构成RL=5，即连续5个1
  - 因此，按极性码的做法保持码流极性平衡，此时应翻转编码，6B=6'b000111，disp=0，这样1011_000111，就不会有RL=5出现了
  - RD=+1+0=+1
- 3B编码：4B=4'b0100，disp=-2，保持极性（当前码流RD=+1），RD=+1-2=-1

4b不完美平衡码举例：

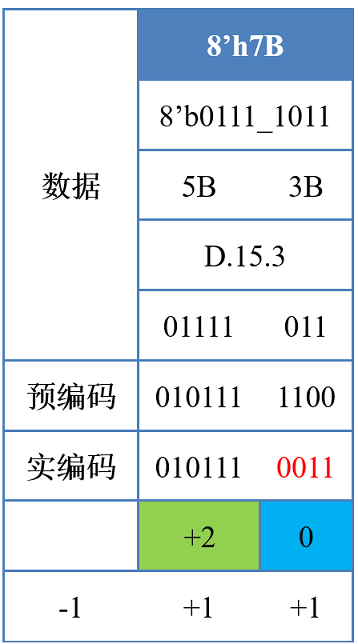
假设发送码流8'7B，初始极性为RD=-1，编码极性简写为disp（disparity）

8'h7B=8'b01111011
- 5B=5'b01111=5'd15，3B=3'b011=3'd3，D.15.3
- 5B编码：6B=6'b010111，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b1100，disp=0
  - 此时，如果按照disp=0，继承码流极性，当前编码不变的话，则前面6B的010111和4B的1100会形成010111_1100，构成RL=5，即连续5个1
  - 因此，按极性码的做法保持码流极性平衡，此时应翻转编码，4B=4'b0011，disp=0，这样010111_0011，就不会有RL=5出现了
  - RD=+1+0=+1

D.x.7

由于D.x.7原始4b编码为1110，其极性为+，另一种码字为0001，其极性为-。

这种码字存在连续的111或者000，可能会与前一个6B的完美平衡码末尾的11或00构成RL=5，因此需要使用备用编码。

D.x.P07：原始4b编码为1110，其极性为+，另一种码字为0001，其极性为-（主要编码）
D.x.A07：原始4b编码为0111，其极性为+，另一种码字为1000，其极性为-（备用编码）

举例：

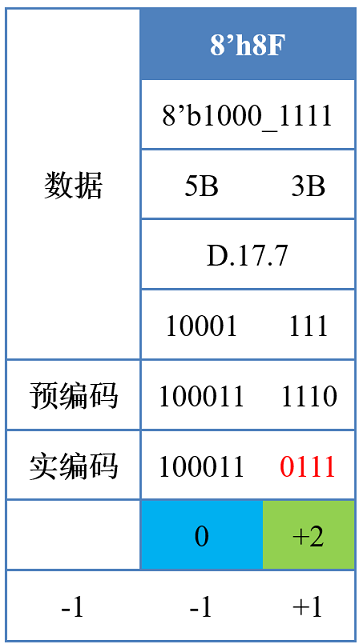
假设发送码流8'h8F，初始极性为RD=-1，编码极性简写为disp（disparity）

8'h8F=8'b10001111
- 5B=5'b10001=5'd17，3B=3'b111=3'd7，D.17.7
- 5B编码：6B=6'b100011，disp=0，继承码流极性，RD=-1+0=-1
- 3B编码：4B=4'b1110，disp=+2
  - 此时，如果按照disp=+2，保持极性（当前码流RD=-1）的话，则前面6B的100011和4B的1110会形成100011_1110，构成RL=5，即连续5个1
  - 但此时不能翻转编码，因为需要保持RD平衡
  - 因此需要disp=+2但没有连续111的码字，即4B=4'b0111，这样100011_0111，就不会有RL=5出现了
  - RD=-1+2=+1

eg_d.x.7.png

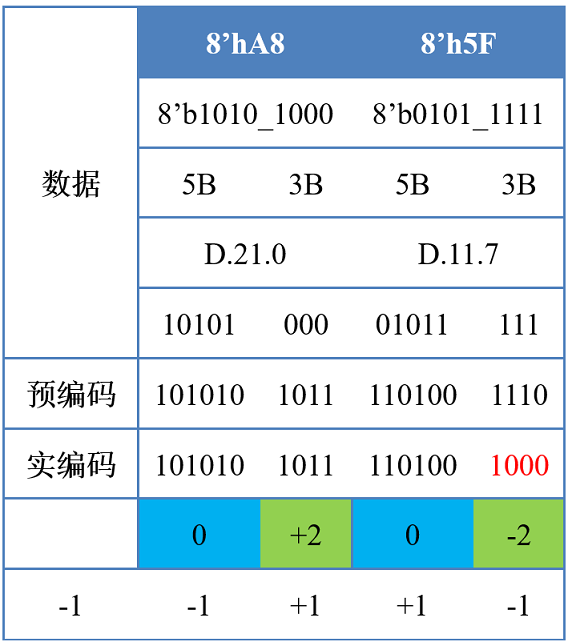
举例：

假设发送码流8'A8,8'5F，初始极性为RD=-1，编码极性简写为disp（disparity）

8'hA8=8'b10101000
- 5B=5'b10101=5'd21，3B=3'b000=3'd0，D.21.0
- 5B编码：6B=6'b101010，disp=0，继承码流极性，RD=-1+0=-1
- 3B编码：4B=4'b1011，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
8'h5F=8'b01011111
- 5B=5'b01011=5'd11，3B=3'b111=3'd7，D.11.7
- 5B编码：6B=6'b110100，disp=0，继承码流极性，RD=+1+0=+1
- 3B编码：4B=4'b1110，disp=+2
  - 此时，如果按照disp=+2，翻转极性（当前码流RD=+1）的话，则前面6B的110100和4B的0001会形成110100_0001，构成RL=5，即连续5个0
  - 但此时不能翻转编码，因为需要保持RD平衡
  - 因此需要disp=-2但没有连续000的码字，即4B=4'b1000，这样100011_1000，就不会有RL=5出现了
  - RD=+1-2=-1

eg2_d.x.7.png

以上所有的控制原则可以保证RL<5，完整的证明8b10b编码RL<5可以参考直流平衡。

示例2

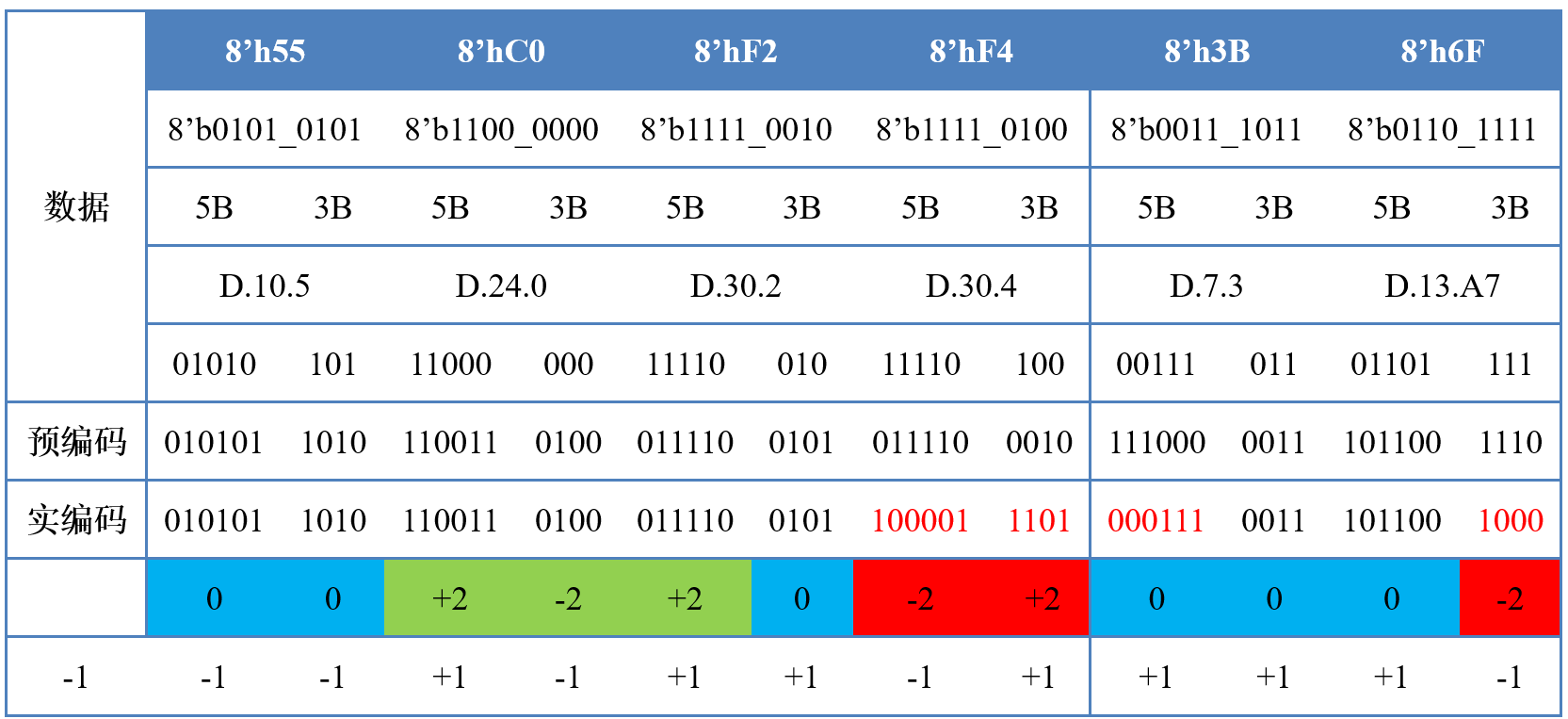
在示例1的基础上，添加8'h3B,8'6F，即发送码流8'h55,8'hC0,8'hF2,8'hF4,8'h3B,8'h6F。

8'h3B=8'b00111011
- 5B=5'b00111=5'd7，3B=3'b011=3'd3，D.7.3
- 5B编码：6B=6'b111000，disp=0，翻转极性（当前码流RD=+1），6B=6'b000111，disp=0，RD=+1+0=+1（不完美平衡码）
- 3B编码：4B=4'b0011，disp=0，继承码流极性，RD=+1+0=+1
8'h6F=8'b01101111
- 5B=5'b01101=5'd13，3B=3'b111=3'd7，D.13.7
- 5B编码：6B=6'b101100，disp=0，继承码流极性，RD=+1+0=+1
- 3B编码：4B=4'b1110，disp=+2，翻转极性（当前码流RD=+1），即4B=4'b0001，但前一个6B存在连续两个0，因此采用备用编码，4B=4'b1000，disp=-2，RD=+1-2=-1

eg2

控制码

控制码（控制字）是用于码流控制的码字，可以作为起始、结尾、分隔，部分码字还可以用于链路同步。

控制码采用与数据码不同的编码方式实现。

5b6b编码表：

5b6b_k

3b4b编码表：

3b4b_k

控制码主要分为两种，下面分别讨论。

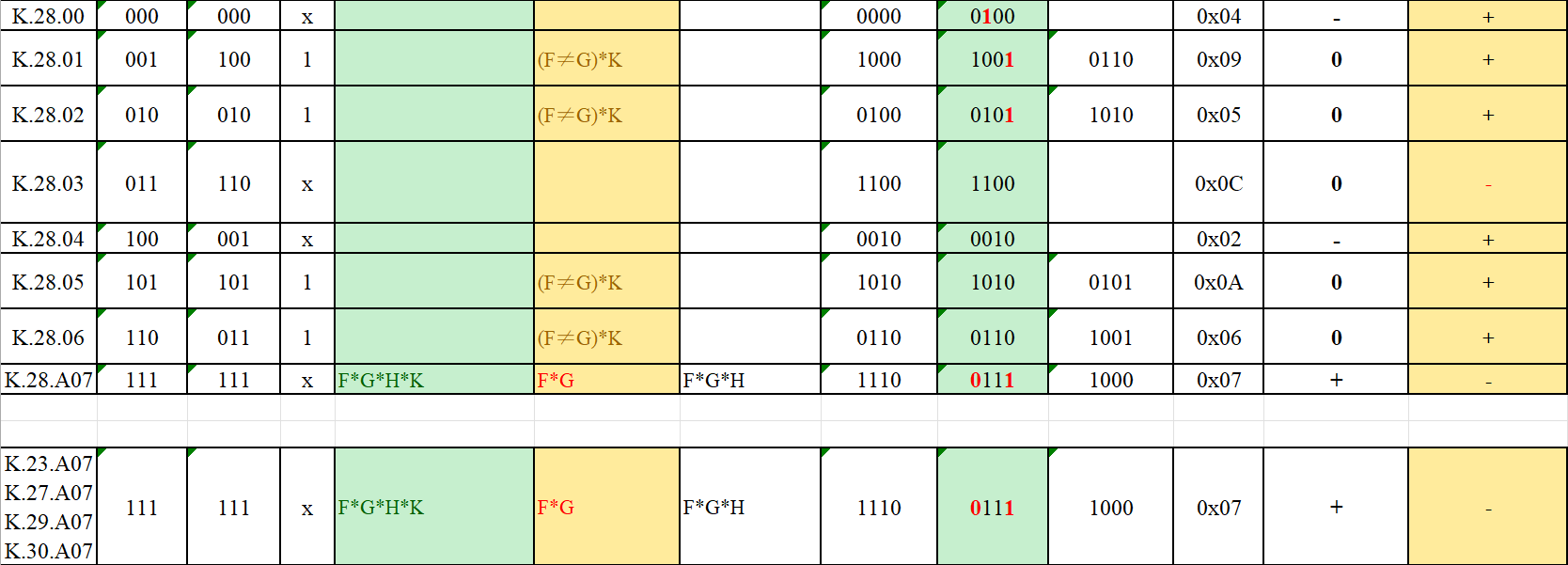
K.28.y

K.28.y是指输入数据5B部分为5b'11100=5'd28类型的控制码。

k28

K.28.y的构造逻辑是5b6b编码表中制造与数据不同的编码方式（数据码中不会出现cdei=1111/0000）。

k.28+d.28

单一性

注意，与数据不同的编码方式仅代表5b6b数据码中不会出现1111/0000，码间仍然可能组合出1111/0000，因此，这种码字在解码端可能会出现混淆。

举例：

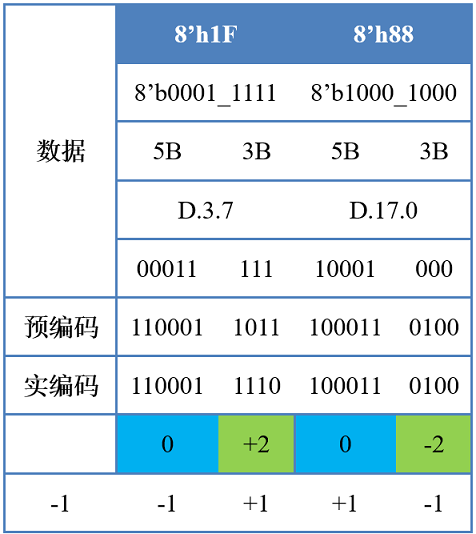
假设发送码流8'h1F,8'h88，初始极性为RD=-1

D.3.7+D.17.0
6B=6'b110001+4B=4'b1110+6B=6'b100011+4B=4'b0100，码流为...1100011110100010100...
可能误识别码流为001111_0100，即K28.0

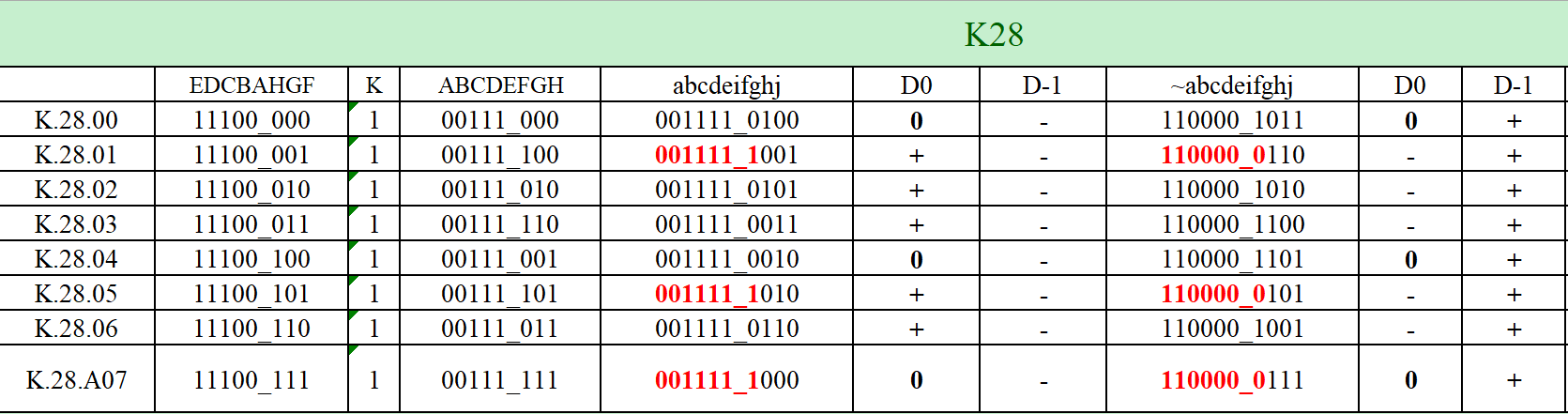
编码图：

sigularity_enc

码流图：

sigularity_flow

可以避免混淆的码字具备单一性（singularity）。

K28.1，K28.5以及K28.7具有特殊的标志位（RL2+RL5，即...0011111...或...1100000...），这在其他码字以及码间都不可能出现
因此，K28.1，K28.5以及K28.7具备单一性（singularity）
K28.1，K28.5以及K28.7也被称为逗号码（comma），只有逗号码可以用于链路同步，因为其他码不具备单一性（singularity）

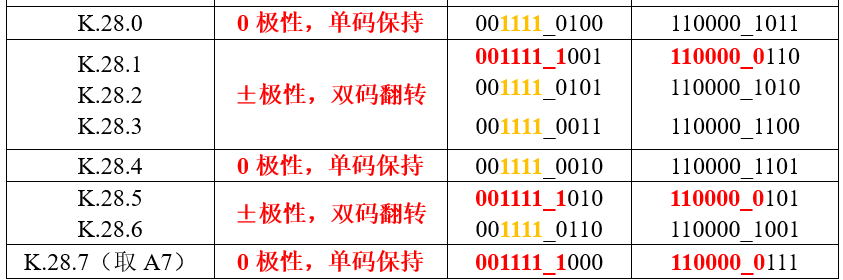
K.28.y 极性

如果连续发送K.28.y，有两种情况：

0极性，单码保持，±码字选择根据上一次rd决定，类似不完美平衡码
±极性，双码翻转

k.28.y_disp

同时，K28.7不能连续发送，会造成连续RL5，即...11111000001111100000...，一般实际使用K28.1，K28.5作为逗号码。

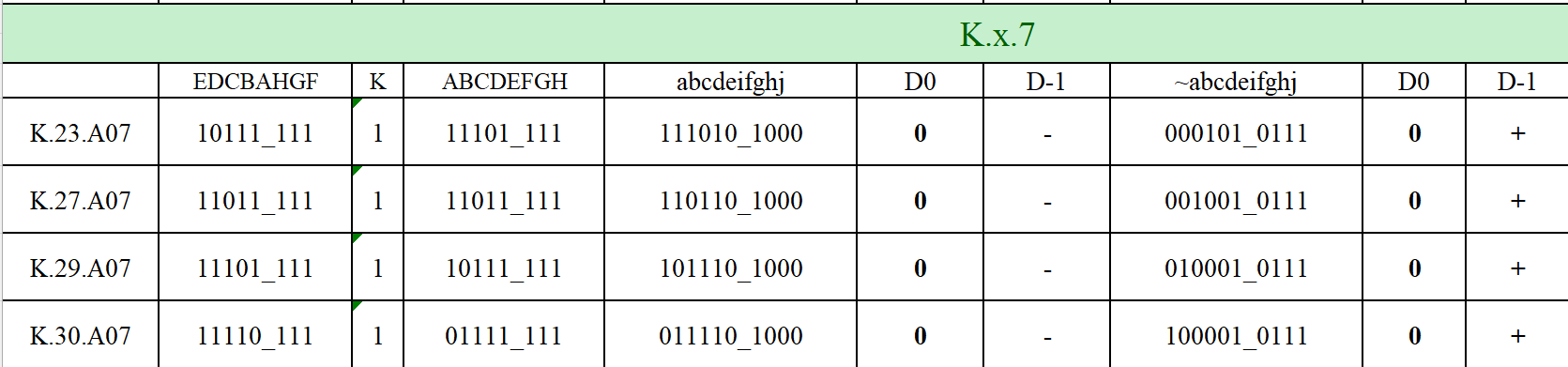
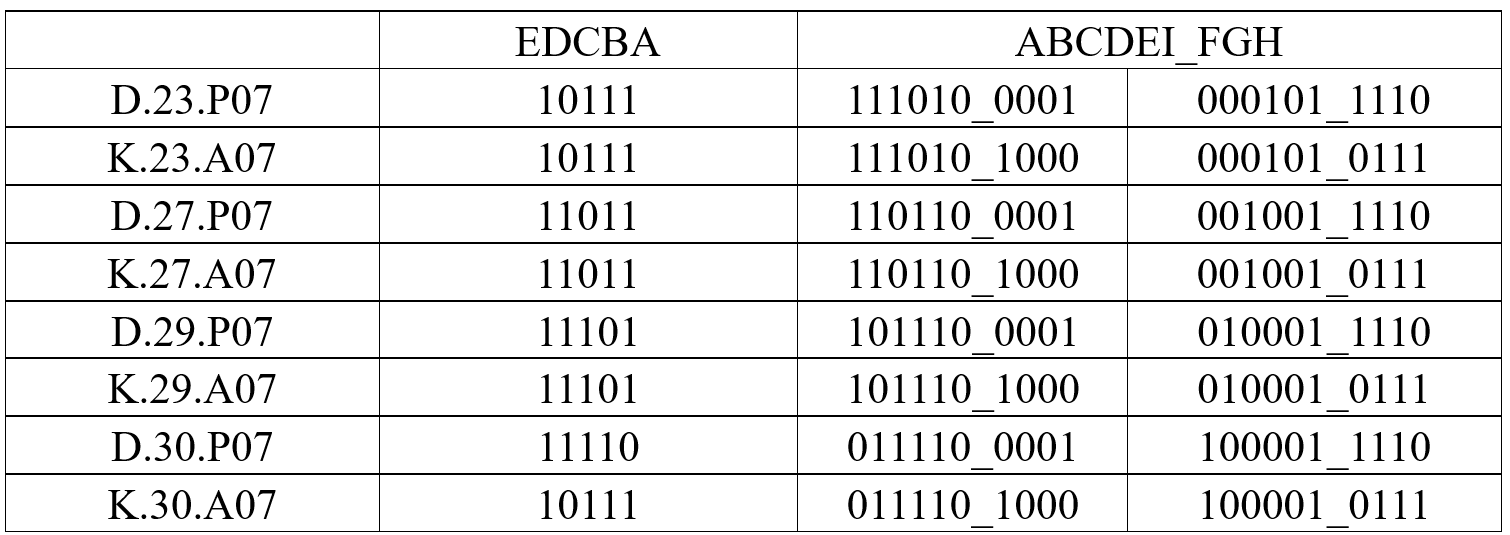
K.x.7

K.x.A07是指输入数据3B部分为3b'111=3'd111类型的控制码。

k.x.7

K.x.A07的构造逻辑是3b4b编码表中制造与数据不同的编码方式（数据码中不会出现eifghj=01_0111/10_1000）。

k.x.7+d.x.7

单一性

同样的，这种码字也不具备单一性（singularity）。这里就不举例了，可以参考K.28.y的例子。

K.x.7 极性

如果连续发送K.x.7，只有单码保持的平衡情况，±码字选择根据上一次rd决定，类似不完美平衡码

k.x.7_disp.png

示例3

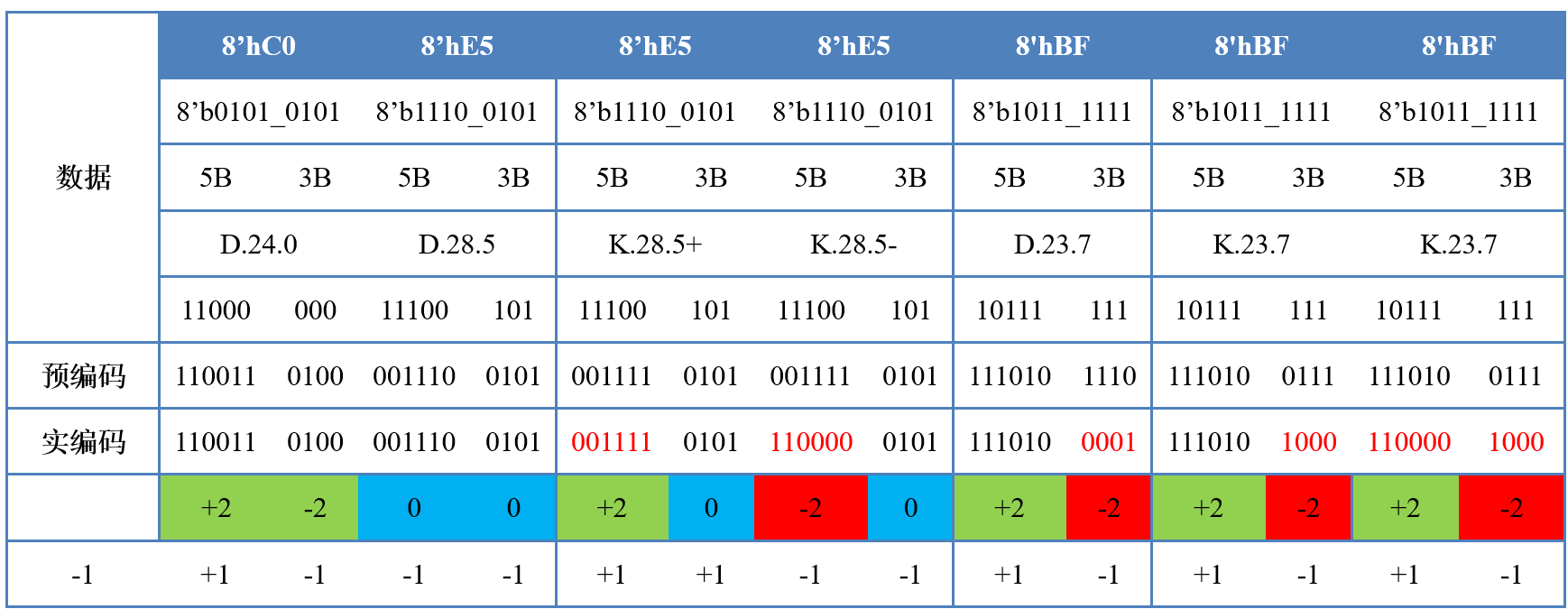
假设发送码流8'hC0,8'hE5,8'hE5(K),8'hE5(K),8'hBF,8'hBF(K),8'hBF(K)，初始极性为RD=-1，编码极性简写为disp（disparity）

8'hC0=8'b11000000
- 5B=5'b11000=5'd24，3B=3'b000=3'd0，D.24.0
- 5B编码：6B=6'b110011，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b0100，disp=-2，保持极性（当前码流RD=+1），RD=+1-2=-1
8'hE5=8'b11100101
- 5B=5'b11100=5'd28，3B=3'b101=3'd5，D.28.5
- 5B编码：6B=6'b001110，disp=0，继承码流极性，RD=-1+0=-1
- 3B编码：4B=4'b1010，disp=0，继承码流极性，RD=-1+0=-1
8'hE5=8'b11100101，K
- 5B=5'b11100=5'd28，3B=3'b101=3'd5，K.28.5
- 5B编码：6B=6'b001111，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b1010，disp=0，继承码流极性，RD=+1+0=+1
- 这种码字可以叫做K.28.5+
8'hE5=8'b11100101，K
- 5B=5'b11100=5'd28，3B=3'b101=3'd5，K.28.5
- 5B编码：6B=6'b001111，disp=+2，翻转极性（当前码流RD=+1），6B=6'b110000，disp=-2，RD=+1-2=-1
- 3B编码：4B=4'b1010，disp=0，继承码流极性，RD=-1+0=-1
- 这种码字可以叫做K.28.5-
8'hBF=8'b10111111
- 5B=5'b10111=5'd23，3B=3'b111=3'd7，D.23.7
- 5B编码：6B=6'b111010，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b1110，disp=+2，翻转极性（当前码流RD=+1），4B=4'b0001，disp=-2，RD=+1-2=-1
8'hBF=8'b10111111，K
- 5B=5'b10111=5'd23，3B=3'b111=3'd7，K.23.7
- 5B编码：6B=6'b111010，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b0111，disp=+2，翻转极性（当前码流RD=+1），4B=4'b1000，disp=-2，RD=+1-2=-1
8'hBF=8'b10111111，K
- 5B=5'b10111=5'd23，3B=3'b111=3'd7，K.23.7
- 5B编码：6B=6'b111010，disp=+2，保持极性（当前码流RD=-1），RD=-1+2=+1
- 3B编码：4B=4'b0111，disp=+2，翻转极性（当前码流RD=+1），4B=4'b1000，disp=-2，RD=+1-2=-1

eg3

直流平衡

下面完整讨论8b10b如何实现直流平衡（dc balance）。首先，在控制原则1中，已经提到了两个方面的考虑：

-2<RD<2，运行极性不超过±2，即总体码流的0,1数量相同
RL<5，运行长度不超过5，即总体码流连续0,1数量不超过5

通过控制原则1已经可以实现-2<RD<2的目标，具体可以参考示例1，示例2和示例3。

因此接下来讨论如何保证RL<5。

RL分析

码内RL
- 观察5b6b编码表，6b编码内部RL<=3;
- 观察3b4b编码表，4b编码内部RL<=3;
因此码内RL<5。
码间RL
- 6b+4b
  - 极性码 + 极性码
    
    6b极性码码间RL<=3，根据控制原则1，4b极性码与6b极性必然相反，因此RL<=3。（e.g. 011000_1110）
  - 极性码 + 平衡码
    
    6b极性码码间RL<=3。
    - 4b如果是完美平衡码，则码间RL<=1，因此总体RL<=4（e.g. 010111_1001）
    - 4b如果是非完美平衡码，根据控制原则2，4b平衡码与6b极性必然相反，因此总体RL<=3（e.g. 010111_0011）
  - 平衡码 + 平衡码
    
    6b平衡码码间RL<=3。
    - 4b如果是完美平衡码，则码间RL<=1，因此总体RL<=4（e.g. 000111_1001）
    - 4b如果是非完美平衡码，根据控制原则2，4b平衡码与6b极性必然相反，因此总体RL<=3（e.g. 111000_1100）
  - 平衡码 + 极性码
    - 6b如果是完美平衡码，则码间RL<=2。4b极性码码间RL<=3。
      - 根据控制原则2，当4b极性码码间RL=3时，4b极性码采用备用编码，因此RL<=2（e.g. 100011_0111）
      - 当4b极性码码间RL<=2时，总体RL<=4（e.g. 100011_1011）
    - 6b如果是非完美平衡码，则码间RL<=3。根据控制原则1，4b极性码与6b极性必然相反，因此RL<=3（e.g. 111000_1110）
- 4b+6b
  - 极性码 + 极性码
    
    4b极性码码间RL<=3，根据控制原则1，6b极性码与4b极性必然相反，因此RL<=3。（e.g. 0111_011000）
  - 极性码 + 平衡码
    
    4b极性码码间RL<=3。
    - 6b如果是完美平衡码，则码间RL<=2，因此总体可能出现RL=5（e.g. 0111_110100）
    - 6b如果是非完美平衡码，根据控制原则2，6b平衡码与4b极性必然相反，因此总体RL<=3（e.g. 0111_000111）
  - 平衡码 + 平衡码
    
    4b平衡码码间RL<=2。
    - 6b如果是完美平衡码，则码间RL<=2，因此总体RL<=4（e.g. 0011_110100）
    - 6b如果是非完美平衡码，根据控制原则2，6b平衡码与4b极性必然相反，因此总体RL<=2（e.g. 1100_111000）
  - 平衡码 + 极性码
    
    4b平衡码码间RL<=2。
    - 4b如果是完美平衡码，则码间RL<=1。6b极性码码间RL<=3。因此RL<=4（e.g. 1010_000110）
    - 4b如果是非完美平衡码，则码间RL<=2。根据控制原则1，6b极性码与4b极性必然相反，因此RL<=2（e.g. 1100_100111）

RL=5

根据上一章的分析，连续出现以下情况会存在RL=5：

完美平衡码，末尾RL=2（e.g. 100011）
D.x.A7 （e.g. 100011_0111）
完美平衡码，首部RL=2。（e.g. 100011_0111_110100）

rl=5

此情况为最极端的情况：

码流前后必为反极性的码字，码流不会出现异常
不会出现连续两次RL=5的情况
不会出现与K码混淆（K.28.y采用的是RL2+RL5，此情况只会出现RL1+RL5）

总体看来，8b10b编码，是直流平衡（dc balance）的，其绝大部分码流RL<=4，最极端情况下RL=5。

电路设计

编码器

5b6b编码

5b6b_d

L 函数

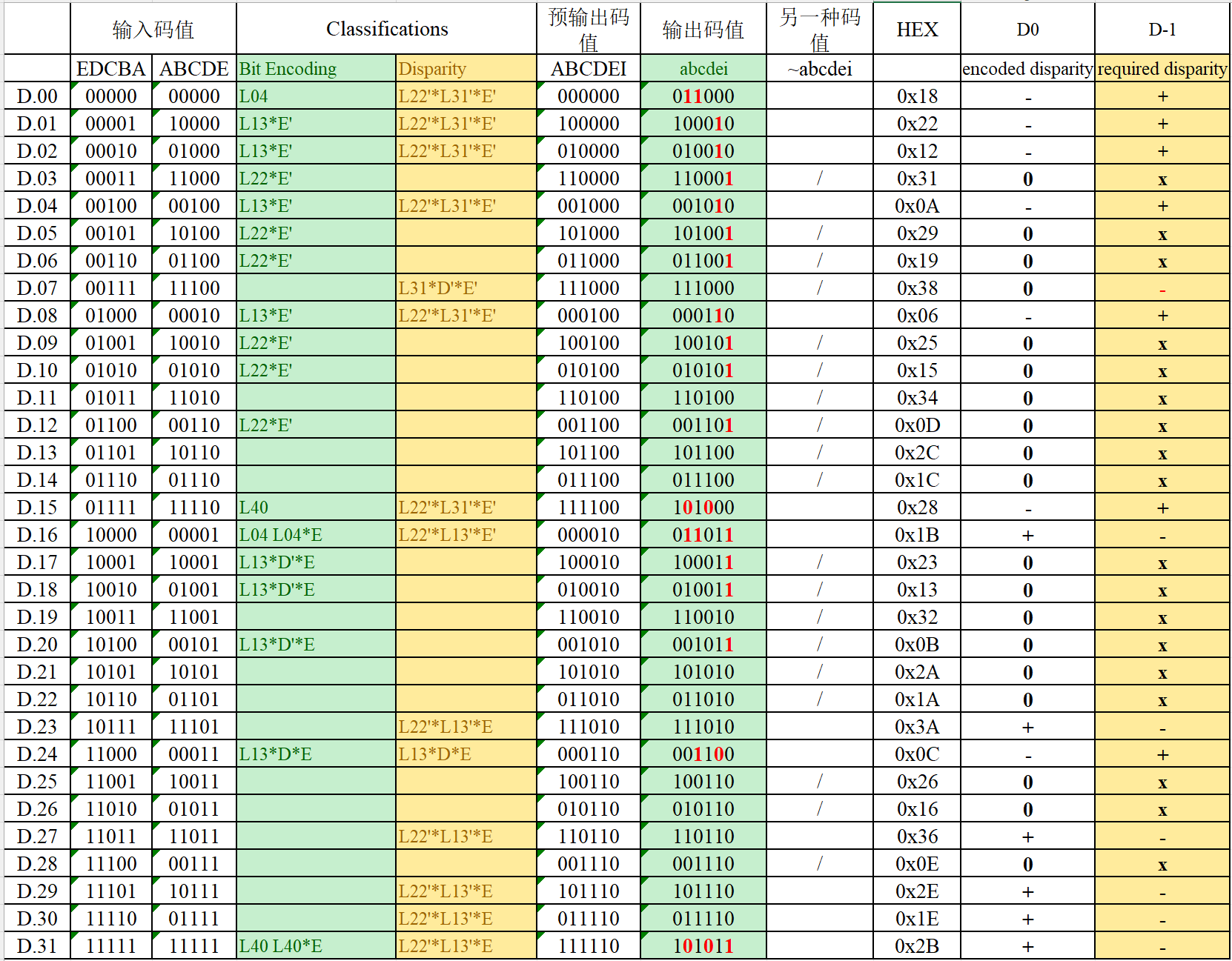
L函数（L function），主要用于化简编码逻辑。观察表格中Bit Encoding列，里面就是L函数。其代表ABCD中的0和1的个数。

举例：

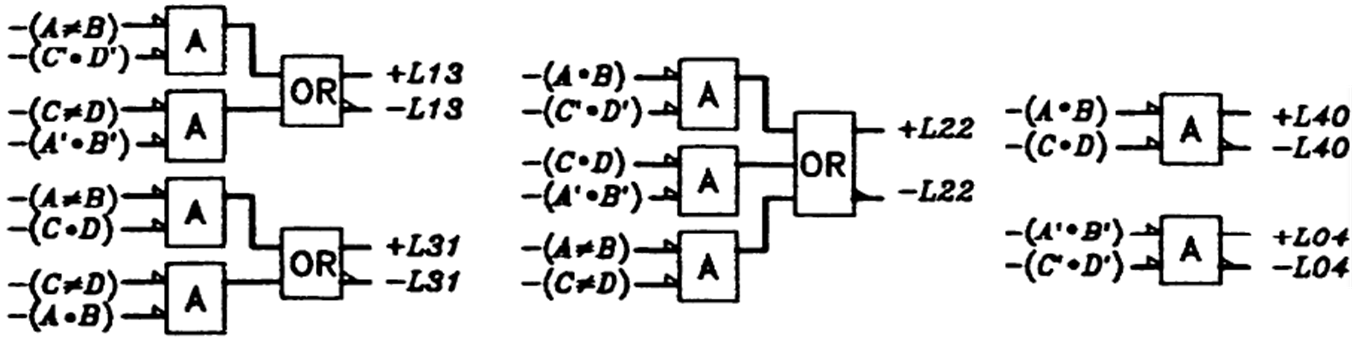
L04：ABCD包含0个1，4个0，即ABCD=0000，因此按布尔逻辑L04=A'B'C'D'
L13：ABCD包含1个1，3个0，即ABCD=1000/ABCD=0100/ABCD=0010/ABCD=0001，因此按布尔逻辑L13=AB'C'D'+A'BC'D'+A'B'CD'+A'B'C'D = (A^B)C'D'+A'B'(C^D)
L22：ABCD包含2个1，2个0，即ABCD=1100/ABCD=1010/ABCD=1001/ABCD=0110/ABCD=0101/ABCD=0011，因此按布尔逻辑L22=ABC'D'+AB'CD'+AB'C'D+A'BCD'+A'BC'D+A'B'CD = ABC'D'+A'B'CD+(A^B)(C^D)

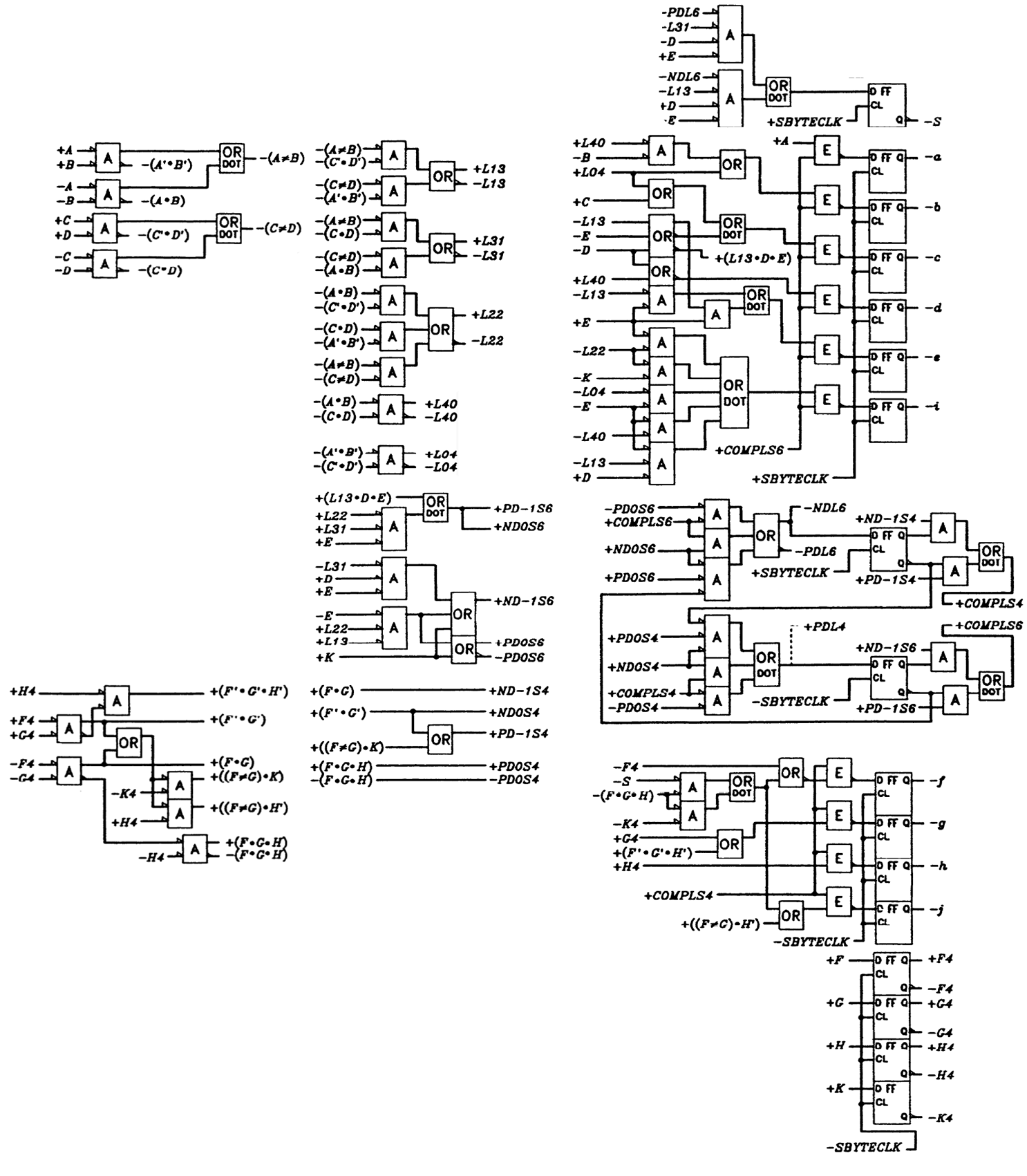
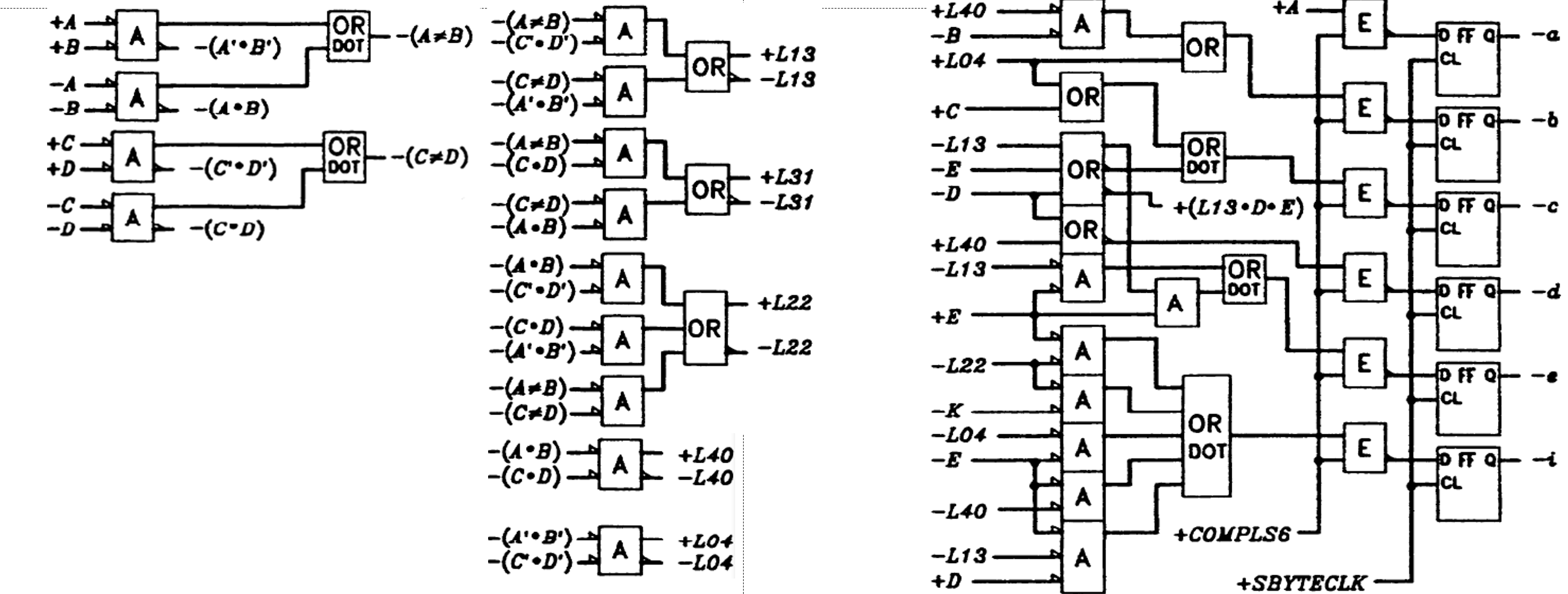
电路图（其中A代表与门，OR代表或门）：

l-function

编码逻辑

EDCBA倒为ABCDE，不需要编码
最后一位I统一补0，形成ABCDEI，不需要编码
根据码表标红比特位编码abcdei（按Bit Encoding）
- 如果从0翻1(强制置1)，则取或
- 如果从1翻0(强制置0)，则取与

举例：

a：观察输出码值列的a，没有标红位置，因此a = A
b：观察输出码值列的b，D.00(L04)，D.15(L40)，D.16(L04)，D.31(L40)有标红位置，根据Bit Encoding列，b = B'L04+BL40' = L04 + BL40'
e：观察输出码值列的e，D.01(L13E')，D.02(L13E')，D.04(L13E')，D.08(L13E')，D.08(L13E')，D.24(L13DE)有标红位置，根据Bit Encoding列，e = E'L13+E(L13DE)'
i：观察输出码值列的i，D.03(L22E')，D.05(L22E')，D.06(L22E')，D.09(L22E')，D.10(L22E')，D.12(L22E')，D.16(L04E)，D.17(L13D'E)，D.18(L22E')，D.20(L22E')，D.31(L40E)有标红位置，根据Bit Encoding列，i = I'(L22E'+L04E+L13D'E+L40E)

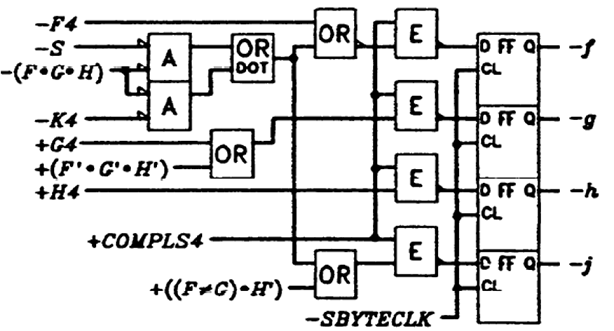
电路图（其中A代表与门，OR代表或门）：

abcdei

3b4b编码

3b4b_d

3b4b编码相对简单，不需要使用L函数（L function）简化逻辑，其编码逻辑与5b6b类似。

fgh-function

另外，由于存在D.x.A07（Alternative，备用码），因此需要编码时加入特殊编码标志（S，Special）。

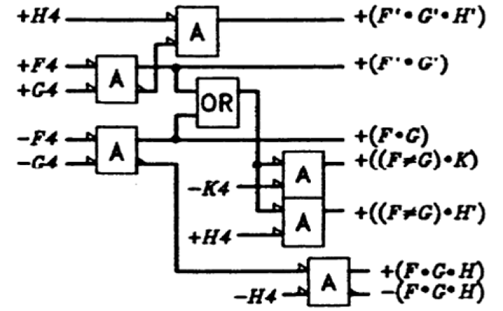
举例：

f：观察输出码值列的f，D.x.A07(FGHS)有标红位置，因此f = F(FGHS)'
g：观察输出码值列的g，D.x.00(F'G'H')有标红位置，根据Bit Encoding列，g = G+G'F'G'H' = G + F'G'H'
j：观察输出码值列的j，D.x.01((F^G)H')，D.x.02((F^G)H')，D.x.A07(FGHS)有标红位置，根据Bit Encoding列，j = E'(F^G)H'+FGHS)+E = (F^G)H' + FGHS + E

电路图（其中A代表与门，OR代表或门）：

fghj

K编码

K.28.y

5b6b_k

同理，根据Bit Encoding列，K.28.y中，i = L22K。电路图参考之前的图。

K.x.7

3b4b_k

同理，根据Bit Encoding列，K.x.7中

f = F(FGHK)'
j = FGHK

电路图参考之前的图。

S编码

特殊的D.x.A07需要单独通过电路实现查找。主要是查找末尾带11/00的完美平衡码e.g. 100011。

special

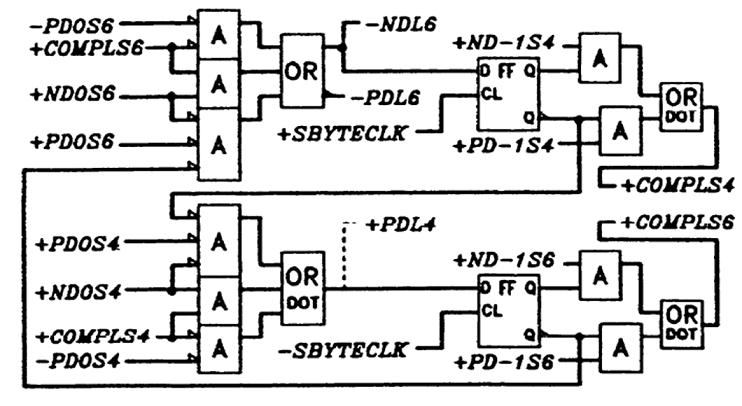
极性编码

注意到极性码以及不完美平衡码是需要翻转极性的，因此需要额外的电路进行实现。

极性计算

实际根据Disparity（D-1）列以及encoded disparity列进行实现。

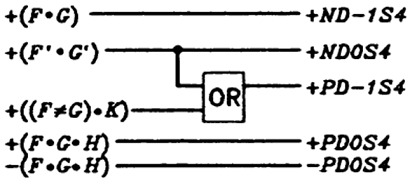
5b6b极性计算：

6bdisp

根据Disparity列以及encoded disparity列，

ND-1S6代表下一编码需要-极性(Negative Disparity)
PD-1S6代表下一编码需要+极性(Positive Disparity)
以上两种都不是，则下一编码需要0极性

另外，

ND0S6代表当前编码为-极性（与PD-1S6相同）
PD0S6代表当前编码为+极性（与ND-1S6不同仅在于不完美平衡码）
以上两种都不是，则当前编码是0极性

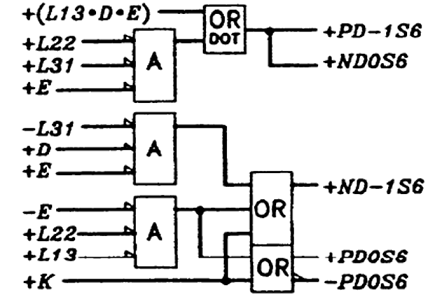
3b4b极性计算：

4bdisp

根据Disparity（D-1）列以及encoded disparity列，

ND-1S4代表下一编码需要-极性(Negative Disparity)
PD-1S4代表下一编码需要+极性(Positive Disparity)
以上两种都不是，则下一编码需要0极性

另外，

ND0S4代表当前编码为-极性（与PD-1S4不同仅在于K码）
PD0S4代表当前编码为+极性（与ND-1S4不同仅在于不完美平衡码）
以上两种都不是，则当前编码是0极性

极性翻转

compls

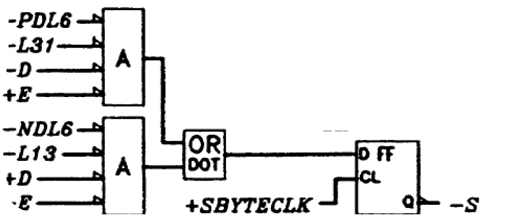
Running Disparity计算（以6b为例，4b同理）：

当前极性为正disp = +2(PD0S6)，不翻转极性（COMPLS6'）,则RD = +1
当前极性为负disp = -2(ND0S6)，翻转极性（COMPLS6）,则RD = +1
当前极性为空disp = 0(PD0S6'ND0S6')，极性继承，则RD = rd(上个编码)

极性翻转计算（以4b为例，6b同理）：

运行极性为正RD = +1，需要极性为负（ND-1S4）,则翻转极性COMPLS4 = +1
运行极性为负RD = -1，需要极性为正（PD-1S4）,则翻转极性COMPLS4 = +1
运行极性为空RD = 0，极性继承，则不翻转极性

电路图

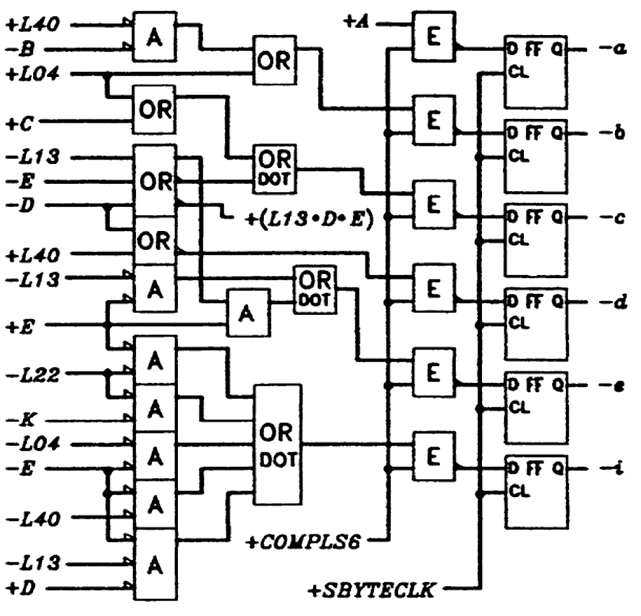
总体电路图架构如下：

architecture

结合上述所有电路，编码器总体电路图如下：

encoder

解码器

解码逻辑

按照编码器的实现逻辑，可以按照解码器的码表进行电路搭建。

注意几点：

解码器收到的码字可能有+或-两种
码表之外的码字代表异常
解码的P函数（P function）类似编码的L函数（L function）

6b5b：

5b6b_dec

4b3b：

3b4b_dec

故障检测

原文给出了故障检测的几种检查方式：

所有码字必须保持+2，-2或0极性
极性码必须调整运行极性
不完美平衡码（D.7以及D.x.3）必须调整运行极性
通信结构中收尾必须含有逗号码
编码异常的电路包含如下（作者总结出来的简化结果）：
- a=b=c=d
- P13e'i'
- P31ei
- f=g=h=j
- e=i=f=g=h
- i≠e=g=h=j
- (e=i≠g=h=j)(c=d=e)'
- P31'ei'g'h'j'
- P13'e'ighj