公式渲染引擎由Mathjax换为Katex,文章可能存在渲染问题,如有发现问题请留言。
前世今生
以下源自参考资料[6] :CORDIC技术并不是什么新鲜的东西。事实上它可以追溯到1957年由J.Volder发表的一篇文章。在上个世纪五十年代,在大型实际的计算机中的实行移位相加受到了当时技术上的限制,所以使用CORDIC变得非常必要。到了七十年代,Hewlett Packard和其他公司出产了手持计算器,许多计算器使用一个内部CORDIC单元来计算所有的三角函数(了解这件事的人们一定还记得,那时求一个角度的正切值需要延迟大约1秒中)。二十世纪八十年代,随着高速度乘法器与带有大存储量的通用处理器的出现,CORDIC算法变得无关紧要了。然而在二十一世纪的今天,对于FPGA来说,CORDIC一定是在DSP应用中(诸如多输入多输出(MIMO),波束形成以及其他自适应系统)计算三角函数的备选技术。
本文将详细介绍CORDIC算法,所有参考资料见文章尾部。
Cordic详解 圆周坐标系 从坐标旋转开始 如下图,一个直角坐标点( x 1 , y 1 ) (x_1,y_1) ( x 1 , y 1 ) θ θ θ ( x 2 , y 2 ) (x_2,y_2) ( x 2 , y 2 ) 如何计算( x 2 , y 2 ) (x_2,y_2) ( x 2 , y 2 )
公式如下:
x 2 = x 1 c o s θ − y 1 c o s θ y 2 = x 1 s i n θ + y 1 c o s θ x_2 = x_1cosθ-y_1cosθ \\
y_2 = x_1sinθ+y_1cosθ
x 2 = x 1 c o s θ − y 1 c o s θ y 2 = x 1 s i n θ + y 1 c o s θ
其实只需要一点高中的知识就能推导这个公式了。
假设底角为α α α 1 1 1
x 2 = c o s ( α + θ ) = c o s ( α ) c o s ( θ ) − s i n ( α ) s i n ( θ ) = x 1 c o s θ − y 1 c o s θ y 2 = s i n ( α + θ ) = s i n ( α ) c o s ( θ ) + c o s ( α ) s i n ( θ ) = x 1 s i n θ + y 1 c o s θ x_2=cos(α+θ) = cos(α)cos(θ) - sin(α)sin(θ) =x_1cosθ-y_1cosθ \\
y_2=sin(α+θ) = sin(α)cos(θ) + cos(α)sin(θ) =x_1sinθ+y_1cosθ
x 2 = c o s ( α + θ ) = c o s ( α ) c o s ( θ ) − s i n ( α ) s i n ( θ ) = x 1 c o s θ − y 1 c o s θ y 2 = s i n ( α + θ ) = s i n ( α ) c o s ( θ ) + c o s ( α ) s i n ( θ ) = x 1 s i n θ + y 1 c o s θ
上面的公式也可以写成矩阵的形式,即
[ x 2 y 2 ] = [ c o s θ − s i n θ s i n θ c o s θ ] [ x 1 y 1 ] \left[
\begin{matrix}
x_2\\
y_2
\end{matrix}
\right]
=
\left[
\begin{matrix}
cosθ&-sinθ\\
sinθ&cosθ
\end{matrix}
\right]
\left[
\begin{matrix}
x_1\\
y_1
\end{matrix}
\right]
[ x 2 y 2 ] = [ c o s θ s i n θ − s i n θ c o s θ ] [ x 1 y 1 ]
以上公式对应逆时针旋转。若是顺时针旋转,则公式应为
[ x 1 y 1 ] = [ c o s θ s i n θ − s i n θ c o s θ ] [ x 2 y 2 ] \left[
\begin{matrix}
x_1\\
y_1
\end{matrix}
\right]
=
\left[
\begin{matrix}
cosθ&sinθ\\
-sinθ&cosθ
\end{matrix}
\right]
\left[
\begin{matrix}
x_2\\
y_2
\end{matrix}
\right]
[ x 1 y 1 ] = [ c o s θ − s i n θ s i n θ c o s θ ] [ x 2 y 2 ]
那么已知旋转角θ θ θ x 2 x_2 x 2 y 2 y_2 y 2 答案就是反复迭代
二分角度旋转
假设( x 1 , y 1 ) = ( 100 , 200 ) (x_1,y_1)=(100,200) ( x 1 , y 1 ) = ( 1 0 0 , 2 0 0 ) ( ρ , θ ) (ρ,θ) ( ρ , θ ) θ θ θ a r c t a n ( y / x ) arctan(y/x) a r c t a n ( y / x ) ( ρ , θ ) = ( 223.61 , 63.435 ) (ρ,θ) = (223.61,63.435) ( ρ , θ ) = ( 2 2 3 . 6 1 , 6 3 . 4 3 5 ) θ θ θ ρ ρ ρ
已知角度在( 0 ° , 90 ° ) (0°,90°) ( 0 ° , 9 0 ° ) 45 ° 45° 4 5 °
[ x y ] = [ c o s ( 45 ° ) s i n ( 45 ° ) − s i n ( 45 ° ) c o s ( 45 ° ) ] [ 100 200 ] = [ 212.13 70.711 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(45°)&sin(45°)\\
-sin(45°)&cos(45°)
\end{matrix}
\right]
\left[
\begin{matrix}
100\\
200
\end{matrix}
\right]
=
\left[
\begin{matrix}
212.13\\
70.711
\end{matrix}
\right]
[ x y ] = [ c o s ( 4 5 ° ) − s i n ( 4 5 ° ) s i n ( 4 5 ° ) c o s ( 4 5 ° ) ] [ 1 0 0 2 0 0 ] = [ 2 1 2 . 1 3 7 0 . 7 1 1 ]
发现纵坐标y > 0 y>0 y > 0 45 / 2 = 22.5 ° 45/2=22.5° 4 5 / 2 = 2 2 . 5 ° 45 + 22.5 = 67.5 ° 45+22.5=67.5° 4 5 + 2 2 . 5 = 6 7 . 5 °
[ x y ] = [ c o s ( 22.5 ° ) s i n ( 22.5 ° ) − s i n ( 22.5 ° ) c o s ( 22.5 ° ) ] [ 212.13 70.711 ] = [ 223.04 − 15.85 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(22.5°)&sin(22.5°)\\
-sin(22.5°)&cos(22.5°)
\end{matrix}
\right]
\left[
\begin{matrix}
212.13\\
70.711
\end{matrix}
\right]
=
\left[
\begin{matrix}
223.04\\
-15.85
\end{matrix}
\right]
[ x y ] = [ c o s ( 2 2 . 5 ° ) − s i n ( 2 2 . 5 ° ) s i n ( 2 2 . 5 ° ) c o s ( 2 2 . 5 ° ) ] [ 2 1 2 . 1 3 7 0 . 7 1 1 ] = [ 2 2 3 . 0 4 − 1 5 . 8 5 ]
发现纵坐标y < 0 y<0 y < 0 22.5 / 2 = 11.25 ° 22.5/2=11.25° 2 2 . 5 / 2 = 1 1 . 2 5 ° 45 + 22.5 − 11.25 = 56.25 ° 45+22.5-11.25=56.25° 4 5 + 2 2 . 5 − 1 1 . 2 5 = 5 6 . 2 5 °
[ x y ] = [ c o s ( 11.25 ° ) − s i n ( 11.25 ° ) s i n ( 11.25 ° ) c o s ( 11.25 ° ) ] [ 223.04 − 15.85 ] = [ 221.85 27.967 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(11.25°)&-sin(11.25°)\\
sin(11.25°)&cos(11.25°)
\end{matrix}
\right]
\left[
\begin{matrix}
223.04\\
-15.85
\end{matrix}
\right]
=
\left[
\begin{matrix}
221.85\\
27.967
\end{matrix}
\right]
[ x y ] = [ c o s ( 1 1 . 2 5 ° ) s i n ( 1 1 . 2 5 ° ) − s i n ( 1 1 . 2 5 ° ) c o s ( 1 1 . 2 5 ° ) ] [ 2 2 3 . 0 4 − 1 5 . 8 5 ] = [ 2 2 1 . 8 5 2 7 . 9 6 7 ]
发现纵坐标y > 0 y>0 y > 0 11.25 / 2 = 5.625 ° 11.25/2=5.625° 1 1 . 2 5 / 2 = 5 . 6 2 5 ° 45 + 22.5 − 11.25 + 5.625 = 61.875 ° 45+22.5-11.25+5.625=61.875° 4 5 + 2 2 . 5 − 1 1 . 2 5 + 5 . 6 2 5 = 6 1 . 8 7 5 °
[ x y ] = [ c o s ( 5.625 ° ) s i n ( 5.625 ° ) − s i n ( 5.625 ° ) c o s ( 5.625 ° ) ] [ 221.85 27.967 ] = [ 223.52 6.0874 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(5.625°)&sin(5.625°)\\
-sin(5.625°)&cos(5.625°)
\end{matrix}
\right]
\left[
\begin{matrix}
221.85\\
27.967
\end{matrix}
\right]
=
\left[
\begin{matrix}
223.52\\
6.0874
\end{matrix}
\right]
[ x y ] = [ c o s ( 5 . 6 2 5 ° ) − s i n ( 5 . 6 2 5 ° ) s i n ( 5 . 6 2 5 ° ) c o s ( 5 . 6 2 5 ° ) ] [ 2 2 1 . 8 5 2 7 . 9 6 7 ] = [ 2 2 3 . 5 2 6 . 0 8 7 4 ]
这时纵坐标已经比较接近0 0 0 ( ρ , θ ) = ( 223.52 , 61.875 ± 5.625 ) (ρ,θ)=(223.52,61.875±5.625) ( ρ , θ ) = ( 2 2 3 . 5 2 , 6 1 . 8 7 5 ± 5 . 6 2 5 ) ( ρ , θ ) = ( 223.61 , 63.435 ) (ρ,θ)=(223.61,63.435) ( ρ , θ ) = ( 2 2 3 . 6 1 , 6 3 . 4 3 5 )
因此通过多次迭代,可以逐渐逼近结果。但是如何计算上面的c o s ( 45 ) , s i n ( 45 ) , c o s ( 22.5 ) , s i n ( 22.5 ) , c o s ( 11.25 ) , s i n ( 11.25 ) cos(45),sin(45),cos(22.5),sin(22.5),cos(11.25),sin(11.25) c o s ( 4 5 ) , s i n ( 4 5 ) , c o s ( 2 2 . 5 ) , s i n ( 2 2 . 5 ) , c o s ( 1 1 . 2 5 ) , s i n ( 1 1 . 2 5 ) 其实如果仔细观察,这些点都是固定的,因此他们的c o s ( ) cos() c o s ( ) s i n ( ) sin() s i n ( ) 所以只需要把要用的点的s i n ( ) sin() s i n ( ) c o s ( ) cos() c o s ( )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 import mathimport numpy as npITERATION_TIMES = 64 i = 0 d = 45 cos = [0 ] * ITERATION_TIMES sin = [0 ] * ITERATION_TIMES degree = [0 ] * ITERATION_TIMES x = 100 y = 200 x_n = 0 y_n = 0 z = 0 for i in range (ITERATION_TIMES): cos[i] = np.cos(d*np.pi/180 ) sin[i] = np.sin(d*np.pi/180 ) degree[i] = d; d = d/2 for i in range (ITERATION_TIMES): if (y>0 ): x_n = x * cos[i] + y * sin[i] y_n = y * cos[i] - x * sin[i] z = z + degree[i] x = x_n y = y_n else : x_n = x * cos[i] - y * sin[i] y_n = y * cos[i] + x * sin[i] z = z - degree[i] x = x_n y = y_n print (z)
经过不同迭代次数,得到不同的结果。迭代次数越高,精度自然就越高。
迭代次数
计算角度(实际结果63.43494882292201)
16
63.433685302734375
32
63.43494881177321
64
63.43494882292201
长度缩放旋转
二分角度旋转的计算存在一个问题:计算量巨大。
每次的旋转公式可以总结为
[ x i + 1 y i + 1 ] = [ c o s ( θ i ) d i s i n ( θ i ) − d i s i n ( θ i ) c o s ( θ i ) ] [ x i y i ] = c o s ( θ i ) [ 1 d i t a n ( θ i ) − d i t a n ( θ i ) 1 ] [ x i y i ] z i + 1 = { z i + θ i , if y i >0 z i − θ i , if y i ≤0 w h e r e d i = { + 1 , if y i >0 − 1 , if y i ≤0 , θ i = 45 ° 2 i \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(θ_i)&d_isin(θ_i)\\
-d_isin(θ_i)&cos(θ_i)
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
=
cos(θ_i)
\left[
\begin{matrix}
1&d_itan(θ_i)\\
-d_itan(θ_i)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
\\
z_{i+1} =
\begin{cases}
z_i + θ_i, & \text{if $y_i$>0} \\
z_i - θ_i, & \text{if $y_i$≤0}
\end{cases}
\\
where\ d_i =
\begin{cases}
+1, & \text{if $y_i$>0} \\
-1, & \text{if $y_i$≤0}
\end{cases}\ ,θ_i=\frac{45°}{2^i}
[ x i + 1 y i + 1 ] = [ c o s ( θ i ) − d i s i n ( θ i ) d i s i n ( θ i ) c o s ( θ i ) ] [ x i y i ] = c o s ( θ i ) [ 1 − d i t a n ( θ i ) d i t a n ( θ i ) 1 ] [ x i y i ] z i + 1 = { z i + θ i , z i − θ i , if y i >0 if y i ≤0 w h e r e d i = { + 1 , − 1 , if y i >0 if y i ≤0 , θ i = 2 i 4 5 °
这样进行转换后可以将c o s ( θ ) cos(θ) c o s ( θ ) 为什么可以将c o s ( θ ) cos(θ) c o s ( θ ) 因为现在的计算只求θ θ θ ρ ρ ρ c o s ( θ ) cos(θ) c o s ( θ )
[ x i + 1 y i + 1 ] = [ 1 d i t a n ( θ i ) − d i t a n ( θ i ) 1 ] [ x i y i ] w h e r e d i = { + 1 , if y i >0 − 1 , if y i ≤0 \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&d_itan(θ_i)\\
-d_itan(θ_i)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
\\
where\ d_i =
\begin{cases}
+1, & \text{if $y_i$>0} \\
-1, & \text{if $y_i$≤0}
\end{cases}
[ x i + 1 y i + 1 ] = [ 1 − d i t a n ( θ i ) d i t a n ( θ i ) 1 ] [ x i y i ] w h e r e d i = { + 1 , − 1 , if y i >0 if y i ≤0
这种旋转方式被称为伪旋转(Pseudo-Rotation)。 t a n ( 45 ) , t a n ( 22.5 ) tan(45),tan(22.5) t a n ( 4 5 ) , t a n ( 2 2 . 5 )
由上方过程演示图对比可以看出,旋转向量的长度在增长,但其旋转角度变化保持与之前一致。Python实现如下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 import mathimport numpy as npITERATION_TIMES = 64 i = 0 d = 45 tan = [0 ] * ITERATION_TIMES degree = [0 ] * ITERATION_TIMES x = 100 y = 200 x_n = 0 y_n = 0 z = 0 for i in range (ITERATION_TIMES): tan[i] = np.tan(d*np.pi/180 ) degree[i] = d; d = d/2 for i in range (ITERATION_TIMES): if (y>0 ): x_n = x + y * tan[i] y_n = y - x * tan[i] z = z + degree[i] x = x_n y = y_n else : x_n = x - y * tan[i] y_n = y + x * tan[i] z = z - degree[i] x = x_n y = y_n print (z)
结果与之前的二分角度旋转一致。
cordic旋转
经过了长度缩放的变换,算法成功将乘法运算减少了一半。那还能不能继续减少运算量呢? 其实依旧可以从之前的长度缩放变换的转换公式入手。
[ x i + 1 y i + 1 ] = [ 1 d i t a n ( θ i ) − d i t a n ( θ i ) 1 ] [ x i y i ] w h e r e d i = { + 1 , if y i >0 − 1 , if y i ≤0 \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&d_itan(θ_i)\\
-d_itan(θ_i)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
where\ d_i=
\begin{cases}
+1, & \text{if $y_i$>0} \\
-1, & \text{if $y_i$≤0}
\end{cases}
[ x i + 1 y i + 1 ] = [ 1 − d i t a n ( θ i ) d i t a n ( θ i ) 1 ] [ x i y i ] w h e r e d i = { + 1 , − 1 , if y i >0 if y i ≤0
第一次旋转45°时,转换公式为
[ x i + 1 y i + 1 ] = [ 1 t a n ( 45 ) − t a n ( 45 ) 1 ] [ x i y i ] = [ 1 1 − 1 1 ] [ x i y i ] \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&tan(45)\\
-tan(45)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&1\\
-1&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
[ x i + 1 y i + 1 ] = [ 1 − t a n ( 4 5 ) t a n ( 4 5 ) 1 ] [ x i y i ] = [ 1 − 1 1 1 ] [ x i y i ]
可见此次转换其实不需要进行乘法运算,可以直接进行加减运算就可以得到结果。然而第二次旋转22.5 ° 22.5° 2 2 . 5 ° t a n ( 22.5 ° ) = 0.4142135623731 tan(22.5°)=0.4142135623731 t a n ( 2 2 . 5 ° ) = 0 . 4 1 4 2 1 3 5 6 2 3 7 3 1 不整的小数。
那有没有办法规避这种复杂乘法? 当然是有的。注意一开始的二分法是通过对45 ° 45° 4 5 ° 22.5 ° 22.5° 2 2 . 5 ° 22.5 ° 22.5° 2 2 . 5 ° 45 ° 45° 4 5 ° t a n ( θ ) = 1 2 tan(θ)=\frac{1}{2} t a n ( θ ) = 2 1 θ θ θ θ = 26.565051177078 ° θ=26.565051177078° θ = 2 6 . 5 6 5 0 5 1 1 7 7 0 7 8 °
[ x i + 1 y i + 1 ] = [ 1 t a n ( 26.565051177078 ° ) − t a n ( 26.565051177078 ° ) 1 ] [ x i y i ] = [ 1 1 2 − 1 2 1 ] [ x i y i ] \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&tan(26.565051177078°)\\
-tan(26.565051177078°)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&\frac{1}{2}\\
-\frac{1}{2}&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
[ x i + 1 y i + 1 ] = [ 1 − t a n ( 2 6 . 5 6 5 0 5 1 1 7 7 0 7 8 ° ) t a n ( 2 6 . 5 6 5 0 5 1 1 7 7 0 7 8 ° ) 1 ] [ x i y i ] = [ 1 − 2 1 2 1 1 ] [ x i y i ]
同样的,每次选择t a n ( θ ) = 1 , 1 2 , 1 4 tan(θ)=1,\frac{1}{2},\frac{1}{4} t a n ( θ ) = 1 , 2 1 , 4 1 在定点运算层面简化了。 1 2 \frac{1}{2} 2 1 1 4 \frac{1}{4} 4 1 复杂的乘法运算转化为了简单的移位和加减运算
[ x i + 1 y i + 1 ] = [ 1 d i t a n ( θ i ) − d i t a n ( θ i ) 1 ] [ x i y i ] = [ 1 d i 2 i − d i 2 i 1 ] [ x i y i ] z i + 1 = { z i + θ i , if y i >0 z i − θ i , if y i ≤0 w h e r e d i = { + 1 , if y i >0 − 1 , if y i ≤0 , θ i = a r c t a n ( 1 2 i ) \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&d_itan(θ_i)\\
-d_itan(θ_i)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&\frac{d_i}{2^i}\\
-\frac{d_i}{2^i}&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
\\
z_{i+1} =
\begin{cases}
z_i + θ_i, & \text{if $y_i$>0} \\
z_i - θ_i, & \text{if $y_i$≤0}
\end{cases}
\\
where\ d_i =
\begin{cases}
+1, & \text{if $y_i$>0} \\
-1, & \text{if $y_i$≤0}
\end{cases}\ ,θ_i=arctan(\frac{1}{2^i})
[ x i + 1 y i + 1 ] = [ 1 − d i t a n ( θ i ) d i t a n ( θ i ) 1 ] [ x i y i ] = [ 1 − 2 i d i 2 i d i 1 ] [ x i y i ] z i + 1 = { z i + θ i , z i − θ i , if y i >0 if y i ≤0 w h e r e d i = { + 1 , − 1 , if y i >0 if y i ≤0 , θ i = a r c t a n ( 2 i 1 )
同样的,可以将θ = a r c t a n ( 1 2 i ) θ=arctan(\frac{1}{2^i}) θ = a r c t a n ( 2 i 1 )
tan(θ)
θ
1
45.0°
0.5
26.56505117707799°
0.25
14.036243467926477°
0.125
7.125016348901798°
0.0625
3.5763343749973515°
0.03125
1.7899106082460694°
0.015625
0.8951737102110744°
…
…
过程演示图如下。
由上方过程演示图对比可以看出,cordic变换向量的长度与长度缩放旋转的变化类似,而其旋转角度发生了根本性变化,使得横纵坐标的变化的小数更整。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 import mathimport numpy as npITERATION_TIMES = 64 i = 0 d = 1 degree = [0 ] * ITERATION_TIMES x = 100 y = 200 x_n = 0 y_n = 0 z = 0 for i in range (ITERATION_TIMES): degree[i] = math.atan(d) d = d/2 d = 1 for i in range (ITERATION_TIMES): if (y>0 ): x_n = x + (y >> d) y_n = y - (x >> d) z = z + degree[i] x = x_n y = y_n else : x_n = x - (y >> d) y_n = y + (x >> d) z = z - degree[i] x = x_n y = y_n d = d >> 1 print (z*180 /np.pi)
至此基本讲清了cordic算法的本质原理(在圆周坐标下)。接下来补充 cordic算法的相关内容。
参数、模式与坐标系 伸缩因子Kn 上一节中只关注了角度θ θ θ ρ ρ ρ cordic旋转公式应还原为(也就是将省略掉的c o s ( θ ) cos(θ) c o s ( θ )
[ x i + 1 y i + 1 ] = [ c o s ( θ i ) d i s i n ( θ i ) − d i s i n ( θ i ) c o s ( θ i ) ] [ x i y i ] = c o s ( θ i ) [ 1 d i t a n ( θ i ) − d i t a n ( θ i ) 1 ] [ x i y i ] = c o s ( θ i ) [ 1 d i 2 i − d i 2 i 1 ] [ x i y i ] z i + 1 = z i + d i θ i w h e r e d i = { + 1 , if y i >0 − 1 , if y i ≤0 , θ i = a r c t a n ( 1 2 i ) \left[
\begin{matrix}
x_{i+1}\\
y_{i+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(θ_i)&d_isin(θ_i)\\
-d_isin(θ_i)&cos(θ_i)
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
=
cos(θ_i)
\left[
\begin{matrix}
1&d_itan(θ_i)\\
-d_itan(θ_i)&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
=
cos(θ_i)
\left[
\begin{matrix}
1&\frac{d_i}{2^i}\\
-\frac{d_i}{2^i}&1
\end{matrix}
\right]
\left[
\begin{matrix}
x_i\\
y_i
\end{matrix}
\right]
\\
z_{i+1} = z_i + d_iθ_i\\
\\
where\ d_i =
\begin{cases}
+1, & \text{if $y_i$>0} \\
-1, & \text{if $y_i$≤0}
\end{cases},\ θ_i = arctan(\frac{1}{2^i})
[ x i + 1 y i + 1 ] = [ c o s ( θ i ) − d i s i n ( θ i ) d i s i n ( θ i ) c o s ( θ i ) ] [ x i y i ] = c o s ( θ i ) [ 1 − d i t a n ( θ i ) d i t a n ( θ i ) 1 ] [ x i y i ] = c o s ( θ i ) [ 1 − 2 i d i 2 i d i 1 ] [ x i y i ] z i + 1 = z i + d i θ i w h e r e d i = { + 1 , − 1 , if y i >0 if y i ≤0 , θ i = a r c t a n ( 2 i 1 )
还原为方程组的形式:
x i + 1 = c o s ( θ i ) ( x i + d i y i t a n ( θ i ) = c o s ( θ i ) ( x i + d i y i 2 i ) y i + 1 = c o s ( θ i ) ( y i − d i x i t a n ( θ i ) = c o s ( θ i ) ( y i − d i x i 2 i ) z i + 1 = z i + d i θ i w h e r e d i = { + 1 , if y i >0 − 1 , if y i ≤0 , θ i = a r c t a n ( 1 2 i ) x_{i+1} = cos(θ_i)(x_i+d_iy_itan(θ_i)=cos(θ_i)(x_i+d_i\frac{y_i}{2^i})\\
y_{i+1} = cos(θ_i)(y_i-d_ix_itan(θ_i)=cos(θ_i)(y_i-d_i\frac{x_i}{2^i})\\
z_{i+1} = z_i + d_iθ_i\\
where\ d_i =
\begin{cases}
+1, & \text{if $y_i$>0} \\
-1, & \text{if $y_i$≤0}
\end{cases}, \ θ_i = arctan(\frac{1}{2^i})\\
x i + 1 = c o s ( θ i ) ( x i + d i y i t a n ( θ i ) = c o s ( θ i ) ( x i + d i 2 i y i ) y i + 1 = c o s ( θ i ) ( y i − d i x i t a n ( θ i ) = c o s ( θ i ) ( y i − d i 2 i x i ) z i + 1 = z i + d i θ i w h e r e d i = { + 1 , − 1 , if y i >0 if y i ≤0 , θ i = a r c t a n ( 2 i 1 )
假设进行64次迭代,则结果计算为
x 64 = ∏ n = 0 63 c o s ( θ n ) ( x n + d y n 2 n ) y 64 = ∏ n = 0 63 c o s ( θ n ) ( y n − d x n 2 n ) z 64 = z 0 + ∑ n = 0 63 d θ n w h e r e { d = + 1 , if y n >0 d = − 1 , if y n ≤0 , θ n = a r c t a n ( 1 2 n ) x_{64} = \prod_{n=0}^{63}cos(θ_n)(x_n+d\frac{y_n}{2^n})\\
y_{64} = \prod_{n=0}^{63}cos(θ_n)(y_n-d\frac{x_n}{2^n})\\
z_{64} = z_0 + \sum_{n=0}^{63}dθ_n \\
where
\begin{cases}
d = +1, & \text{if $y_n$>0} \\
d = -1, & \text{if $y_n$≤0}
\end{cases},\ θ_n = arctan(\frac{1}{2^n})\\
x 6 4 = n = 0 ∏ 6 3 c o s ( θ n ) ( x n + d 2 n y n ) y 6 4 = n = 0 ∏ 6 3 c o s ( θ n ) ( y n − d 2 n x n ) z 6 4 = z 0 + n = 0 ∑ 6 3 d θ n w h e r e { d = + 1 , d = − 1 , if y n >0 if y n ≤0 , θ n = a r c t a n ( 2 n 1 )
可以发现其实迭代过程的计算分为两部分,一部分是cordic的旋转变换,一部分是cordic的长度伸缩变换。
cordic长度伸缩变换:
∏ n = 0 63 c o s ( θ n ) \prod_{n=0}^{63}cos(θ_n)
n = 0 ∏ 6 3 c o s ( θ n )
cordic旋转变换:
∏ n = 0 63 ( x n + d y n 2 n ) ∏ n = 0 63 ( y n − d x n 2 n ) w h e r e { d = + 1 , if y n >0 d = − 1 , if y n ≤0 \prod_{n=0}^{63}(x_n+d\frac{y_n}{2^n})\\
\prod_{n=0}^{63}(y_n-d\frac{x_n}{2^n})\\
where
\begin{cases}
d = +1, & \text{if $y_n$>0} \\
d = -1, & \text{if $y_n$≤0}
\end{cases}
n = 0 ∏ 6 3 ( x n + d 2 n y n ) n = 0 ∏ 6 3 ( y n − d 2 n x n ) w h e r e { d = + 1 , d = − 1 , if y n >0 if y n ≤0
由于在cordic旋转变换中,已知θ n = a r c t a n ( 1 2 n ) θ_n=arctan(\frac{1}{2^n}) θ n = a r c t a n ( 2 n 1 )
∏ n = 0 63 ( c o s ( θ n ) ) = ∏ n = 0 63 ( 1 1 + t a n 2 ( θ n ) ) = ∏ n = 0 63 ( 1 1 + ( 1 2 n ) 2 ) \prod_{n=0}^{63}(cos(θ_n))=\prod_{n=0}^{63}(\sqrt{\frac{1}{1+tan^2(θ_n)}})=\prod_{n=0}^{63}(\sqrt{\frac{1}{1+(\frac{1}{2^n})^2}})
n = 0 ∏ 6 3 ( c o s ( θ n ) ) = n = 0 ∏ 6 3 ( 1 + t a n 2 ( θ n ) 1 ) = n = 0 ∏ 6 3 ( 1 + ( 2 n 1 ) 2 1 )
当n → ∞ n\to∞ n → ∞ 乘以收敛值的倒数以恢复 伸缩因子K n K_n K n
K n = lim n → ∞ ( ∏ 0 n ( 1 + ( 1 2 n ) 2 ) ) ≈ 1.64676 1 K n ≈ 0.6073 K_n=\lim_{n\to∞}(\prod_{0}^{n}(\sqrt{1+(\frac{1}{2^n})^2}))≈1.64676 \\
\frac{1}{K_n}≈ 0.6073
K n = n → ∞ lim ( 0 ∏ n ( 1 + ( 2 n 1 ) 2 ) ) ≈ 1 . 6 4 6 7 6 K n 1 ≈ 0 . 6 0 7 3
通过下表可见伸缩因子随迭代次数的变化
迭代次数
伸缩因子Kn
10
1.646759211139822
20
1.6467602581200669
50
1.6467602581210652
100
1.6467602581210652
可见伸缩因子随着迭代次数增加而变化越来越小,最终收敛。这样可以利用cordic旋转后通过乘以伸缩因子来保证长度变换也是正确的,从而求到长度ρ ρ ρ
x n + 1 = K n ∏ n = 0 n ( x n + d y n 2 n ) y n + 1 = K n ∏ n = 0 n ( y n − d x n 2 n ) z n + 1 = z 0 + ∑ n = 0 n d θ n w h e r e { d = + 1 , if y n >0 d = − 1 , if y n ≤0 , θ n = a r c t a n ( 1 2 n ) x_{n+1} = K_n\prod_{n=0}^{n}(x_n+d\frac{y_n}{2^n})\\
y_{n+1} = K_n\prod_{n=0}^{n}(y_n-d\frac{x_n}{2^n})\\
z_{n+1} = z_0 + \sum_{n=0}^{n}dθ_n\\
where
\begin{cases}
d = +1, & \text{if $y_n$>0} \\
d = -1, & \text{if $y_n$≤0}
\end{cases},\ θ_n = arctan(\frac{1}{2^n})\\
x n + 1 = K n n = 0 ∏ n ( x n + d 2 n y n ) y n + 1 = K n n = 0 ∏ n ( y n − d 2 n x n ) z n + 1 = z 0 + n = 0 ∑ n d θ n w h e r e { d = + 1 , d = − 1 , if y n >0 if y n ≤0 , θ n = a r c t a n ( 2 n 1 )
两种旋转模式 在圆周坐标系下的坐标旋转其实存在两个问题:
已知x 1 x_1 x 1 y 1 y_1 y 1 如何计算旋转角θ θ θ y = 0 y=0 y = 0
已知旋转角θ θ θ x 1 x_1 x 1 y 1 = 0 y_1=0 y 1 = 0 如何计算x 2 x_2 x 2 y 2 y_2 y 2
这是两个镜像问题
通过不断进行cordic旋转变换逼近y = 0 y=0 y = 0 y = 0 y=0 y = 0
使结果纵坐标y → 0 y\to0 y → 0 cordic旋转变换称为向量模式(vector mode)
通过不断进行cordic旋转变换逼近旋转角θ θ θ θ = 0 θ=0 θ = 0
使结果角度θ → 0 θ\to0 θ → 0 cordic旋转变换被称为旋转模式(rotation mode)
圆周坐标的向量模式(vector mode)的公式为(上一节已经推导)
迭代式:
{ x i + 1 = x i + d i y i 2 i y i + 1 = y i − d i x i 2 i z i + 1 = z i + d θ i w h e r e { d i = + 1 , if y i >0 d i = − 1 , if y i ≤0 , θ i = a r c t a n ( 1 2 i ) \begin{cases}
x_{i+1} = x_i+d_i\frac{y_i}{2^i}\\
y_{i+1} = y_i-d_i\frac{x_i}{2^i}\\
z_{i+1} = z_i + dθ_i\\
\end{cases}
\\
where
\begin{cases}
d_i = +1, & \text{if $y_i$>0} \\
d_i = -1, & \text{if $y_i$≤0}
\end{cases},θ_i = arctan(\frac{1}{2^i})\\
⎩ ⎪ ⎨ ⎪ ⎧ x i + 1 = x i + d i 2 i y i y i + 1 = y i − d i 2 i x i z i + 1 = z i + d θ i w h e r e { d i = + 1 , d i = − 1 , if y i >0 if y i ≤0 , θ i = a r c t a n ( 2 i 1 )
结果式:
x n + 1 = K n ∏ n = 0 n ( x n + d y n 2 n ) y n + 1 = K n ∏ n = 0 n ( y n − d x n 2 n ) z n + 1 = z 0 + ∑ n = 0 n d θ n w h e r e { d = + 1 , if y n >0 d = − 1 , if y n ≤0 , θ n = a r c t a n ( 1 2 n ) x_{n+1} = K_n\prod_{n=0}^{n}(x_n+d\frac{y_n}{2^n})\\
y_{n+1} = K_n\prod_{n=0}^{n}(y_n-d\frac{x_n}{2^n})\\
z_{n+1} = z_0 + \sum_{n=0}^{n}dθ_n
\\
where
\begin{cases}
d = +1, & \text{if $y_n$>0} \\
d = -1, & \text{if $y_n$≤0}
\end{cases},\ θ_n = arctan(\frac{1}{2^n})\\
x n + 1 = K n n = 0 ∏ n ( x n + d 2 n y n ) y n + 1 = K n n = 0 ∏ n ( y n − d 2 n x n ) z n + 1 = z 0 + n = 0 ∑ n d θ n w h e r e { d = + 1 , d = − 1 , if y n >0 if y n ≤0 , θ n = a r c t a n ( 2 n 1 )
圆周坐标下旋转模式(rotation mode)的公式为
迭代式:
{ x i + 1 = x i − d i y i 2 i y i + 1 = y i + d i x i 2 i z i + 1 = z i − d i θ i w h e r e { d i = + 1 , if z i >0 d i = − 1 , if z i ≤0 , θ i = a r c t a n ( 1 2 i ) \begin{cases}
x_{i+1} = x_i-d_i\frac{y_i}{2^i}\\
y_{i+1} = y_i+d_i\frac{x_i}{2^i}\\
z_{i+1} = z_i - d_iθ_i\\
\end{cases}
\\
where
\begin{cases}
d_i = +1, & \text{if $z_i$>0} \\
d_i = -1, & \text{if $z_i$≤0}
\end{cases},θ_i = arctan(\frac{1}{2^i})\\
⎩ ⎪ ⎨ ⎪ ⎧ x i + 1 = x i − d i 2 i y i y i + 1 = y i + d i 2 i x i z i + 1 = z i − d i θ i w h e r e { d i = + 1 , d i = − 1 , if z i >0 if z i ≤0 , θ i = a r c t a n ( 2 i 1 )
结果式:
x n + 1 = K n ∏ n = 0 n ( x n − d y n 2 n ) y n + 1 = K n ∏ n = 0 n ( y n + d x n 2 n ) z n + 1 = z 0 − ∑ n = 0 n d θ n w h e r e { d = + 1 , if z n >0 d = − 1 , if z n ≤0 , θ n = a r c t a n ( 1 2 n ) x_{n+1} = K_n\prod_{n=0}^{n}(x_n-d\frac{y_n}{2^n})\\
y_{n+1} = K_n\prod_{n=0}^{n}(y_n+d\frac{x_n}{2^n})\\
z_{n+1} = z_0 - \sum_{n=0}^{n}dθ_n\\
where
\begin{cases}
d = +1, & \text{if $z_n$>0} \\
d = -1, & \text{if $z_n$≤0}
\end{cases},\ θ_n = arctan(\frac{1}{2^n})\\
x n + 1 = K n n = 0 ∏ n ( x n − d 2 n y n ) y n + 1 = K n n = 0 ∏ n ( y n + d 2 n x n ) z n + 1 = z 0 − n = 0 ∑ n d θ n w h e r e { d = + 1 , d = − 1 , if z n >0 if z n ≤0 , θ n = a r c t a n ( 2 n 1 )
三种坐标系 上文只讨论了圆周坐标系,实际cordic算法可用于三种坐标系,进行不同的复杂运算。
圆周坐标系(circular rotations) 线性坐标系(linear rotations) 双曲线坐标系(hyperbolic rotations)
圆周坐标系
之前的所有讨论均基于圆周坐标系。这里不再赘述。
线性坐标系
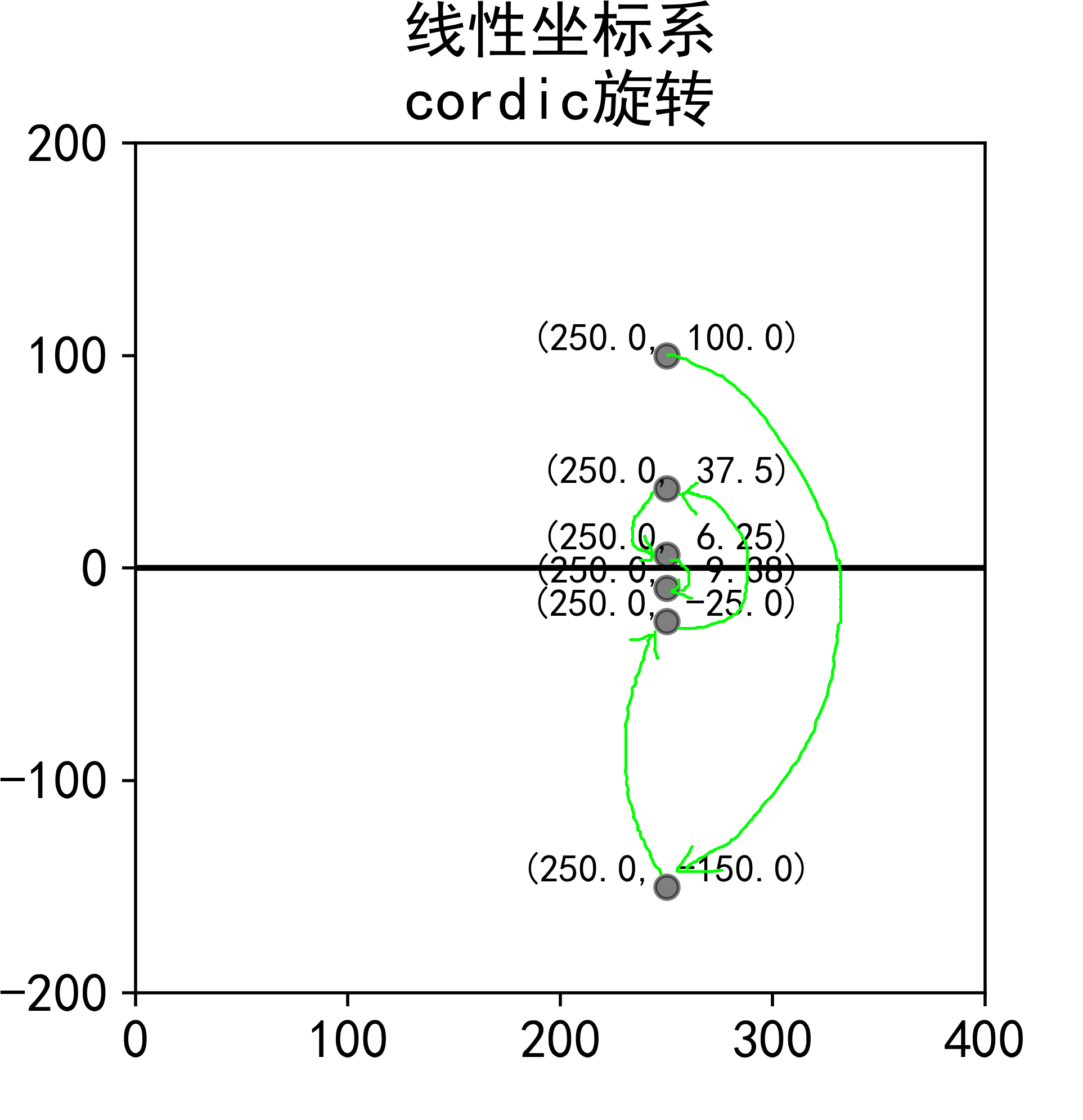
假设( x 1 , y 1 ) = ( 250 , 100 ) (x_1,y_1)=(250,100) ( x 1 , y 1 ) = ( 2 5 0 , 1 0 0 ) θ θ θ t a n θ = 2 5 tanθ=\frac{2}{5} t a n θ = 5 2 cordic旋转算法进行尝试。
类似的,先逆时针"旋转"45 ° 45° 4 5 ° x 2 = x 1 = 100 x_2=x_1=100 x 2 = x 1 = 1 0 0 y 2 = y 1 − x 1 t a n 45 ° = y 1 − x 1 y_2=y_1-x_1tan45°=y_1-x_1 y 2 = y 1 − x 1 t a n 4 5 ° = y 1 − x 1
[ x y ] = [ 1 0 − t a n ( 45 ° ) 1 ] [ 250 100 ] = [ 1 0 − 1 1 ] [ 250 100 ] = [ 250 − 150 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
-tan(45°)&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
100
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
-1&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
100
\end{matrix}
\right]
=
\left[
\begin{matrix}
250\\
-150
\end{matrix}
\right]
[ x y ] = [ 1 − t a n ( 4 5 ° ) 0 1 ] [ 2 5 0 1 0 0 ] = [ 1 − 1 0 1 ] [ 2 5 0 1 0 0 ] = [ 2 5 0 − 1 5 0 ]
发现纵坐标y < 0 y<0 y < 0 t a n ( θ ) = 1 2 tan(θ)=\frac{1}{2} t a n ( θ ) = 2 1 θ θ θ θ = 26.565051177078 ° θ=26.565051177078° θ = 2 6 . 5 6 5 0 5 1 1 7 7 0 7 8 °
[ x y ] = [ 1 0 t a n ( 26.565051177078 ° ) 1 ] [ 250 − 150 ] = [ 1 0 1 2 1 ] [ 250 − 150 ] = [ 250 − 25 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
tan(26.565051177078°)&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
-150
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
\frac{1}{2}&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
-150
\end{matrix}
\right]
=
\left[
\begin{matrix}
250\\
-25
\end{matrix}
\right]
[ x y ] = [ 1 t a n ( 2 6 . 5 6 5 0 5 1 1 7 7 0 7 8 ° ) 0 1 ] [ 2 5 0 − 1 5 0 ] = [ 1 2 1 0 1 ] [ 2 5 0 − 1 5 0 ] = [ 2 5 0 − 2 5 ]
发现纵坐标y < 0 y<0 y < 0 t a n ( θ ) = 1 4 tan(θ)=\frac{1}{4} t a n ( θ ) = 4 1 θ θ θ θ = 14.036243467926477 ° θ=14.036243467926477° θ = 1 4 . 0 3 6 2 4 3 4 6 7 9 2 6 4 7 7 °
[ x y ] = [ 1 0 t a n ( 14.036243467926477 ° ) 1 ] [ 250 − 25 ] = [ 1 0 1 4 1 ] [ 250 − 25 ] = [ 250 37.5 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
tan(14.036243467926477°)&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
-25
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
\frac{1}{4}&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
-25
\end{matrix}
\right]
=
\left[
\begin{matrix}
250\\
37.5
\end{matrix}
\right]
[ x y ] = [ 1 t a n ( 1 4 . 0 3 6 2 4 3 4 6 7 9 2 6 4 7 7 ° ) 0 1 ] [ 2 5 0 − 2 5 ] = [ 1 4 1 0 1 ] [ 2 5 0 − 2 5 ] = [ 2 5 0 3 7 . 5 ]
发现纵坐标y > 0 y>0 y > 0 t a n ( θ ) = 1 8 tan(θ)=\frac{1}{8} t a n ( θ ) = 8 1 θ θ θ θ = 7.125016348901798 ° θ=7.125016348901798° θ = 7 . 1 2 5 0 1 6 3 4 8 9 0 1 7 9 8 °
[ x y ] = [ 1 0 − t a n ( 7.125016348901798 ° ) 1 ] [ 250 37.5 ] = [ 1 0 − 1 8 1 ] [ 250 37.5 ] = [ 250 6.25 ] \left[
\begin{matrix}
x\\
y
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
-tan(7.125016348901798°)&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
37.5
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0\\
-\frac{1}{8}&1
\end{matrix}
\right]
\left[
\begin{matrix}
250\\
37.5
\end{matrix}
\right]
=
\left[
\begin{matrix}
250\\
6.25
\end{matrix}
\right]
[ x y ] = [ 1 − t a n ( 7 . 1 2 5 0 1 6 3 4 8 9 0 1 7 9 8 ° ) 0 1 ] [ 2 5 0 3 7 . 5 ] = [ 1 − 8 1 0 1 ] [ 2 5 0 3 7 . 5 ] = [ 2 5 0 6 . 2 5 ]
这时纵坐标已经比较接近0 0 0 ( x , y ) = ( 250 , 6.25 ± 15.625 ) (x,y)=(250,6.25±15.625) ( x , y ) = ( 2 5 0 , 6 . 2 5 ± 1 5 . 6 2 5 ) ( x , y ) = ( 250 , 0 ) (x,y)=(250,0) ( x , y ) = ( 2 5 0 , 0 )
线性坐标系的"旋转"其实与圆周坐标系下的旋转含义并不相同了,因为这里的矩阵变化(所谓旋转)其实表现的就是一种迭代映射,其变换逻辑图如下:
注意,上述讨论分析的是使结果纵坐标y → 0 y\to0 y → 0 cordic旋转变换,因此是向量模式(vector mode)
线性坐标的向量模式(vector mode)的公式为(根据上述内容推导,z z z t a n ( y 1 / x 1 ) tan(y1/x1) t a n ( y 1 / x 1 ) cordic算法规定迭代n从1开始,且由于没有迭代乘法,并不存在伸缩因子K n K_n K n
迭代式:
{ x i + 1 = x i y i + 1 = y i − d i x i 2 i z i + 1 = z i + d i x i 2 i w h e r e { d i = + 1 , if y i >0 d i = − 1 , if y i ≤0 \begin{cases}
x_{i+1} = x_i\\
y_{i+1} = y_i - d_i\frac{x_i}{2^i}\\
z_{i+1} = z_i + d_i\frac{x_i}{2^i}\\
\end{cases}
\\
where
\begin{cases}
d_i = +1, & \text{if $y_i$>0} \\
d_i = -1, & \text{if $y_i$≤0}
\end{cases}
⎩ ⎪ ⎨ ⎪ ⎧ x i + 1 = x i y i + 1 = y i − d i 2 i x i z i + 1 = z i + d i 2 i x i w h e r e { d i = + 1 , d i = − 1 , if y i >0 if y i ≤0
结果式:
x n + 1 = x n = x 0 y n + 1 = y 0 − ∑ n = 0 n d x n 2 n z n + 1 = z 0 + ∑ n = 1 n d 2 n w h e r e { d = + 1 , if y n >0 d = − 1 , if y n ≤0 x_{n+1} = x_n = x_0\\
y_{n+1} = y_0 - \sum_{n=0}^{n}\frac{dx_n}{2^n}\\
z_{n+1} = z_0 + \sum_{n=1}^{n}\frac{d}{2^n}
\\
where
\begin{cases}
d = +1, & \text{if $y_n$>0} \\
d = -1, & \text{if $y_n$≤0}
\end{cases}
x n + 1 = x n = x 0 y n + 1 = y 0 − n = 0 ∑ n 2 n d x n z n + 1 = z 0 + n = 1 ∑ n 2 n d w h e r e { d = + 1 , d = − 1 , if y n >0 if y n ≤0
圆周坐标下旋转模式(rotation mode)的公式为
迭代式:
{ x i + 1 = x i y i + 1 = y i + d x i 2 i z i + 1 = z i − d x i 2 i w h e r e { d = + 1 , if z i >0 d = − 1 , if z i ≤0 \begin{cases}
x_{i+1} = x_i\\
y_{i+1} = y_i + d\frac{x_i}{2^i}\\
z_{i+1} = z_i - d\frac{x_i}{2^i}\\
\end{cases}
\\
where
\begin{cases}
d = +1, & \text{if $z_i$>0} \\
d = -1, & \text{if $z_i$≤0}
\end{cases}
⎩ ⎪ ⎨ ⎪ ⎧ x i + 1 = x i y i + 1 = y i + d 2 i x i z i + 1 = z i − d 2 i x i w h e r e { d = + 1 , d = − 1 , if z i >0 if z i ≤0
结果式:
x n + 1 = x n = x 0 y n + 1 = y 0 + ∑ n = 0 n d x n 2 n z n + 1 = z 0 − ∑ n = 1 n d 2 n w h e r e { d = + 1 , if z n >0 d = − 1 , if z n ≤0 x_{n+1} = x_n = x_0\\
y_{n+1} = y_0 + \sum_{n=0}^{n}\frac{dx_n}{2^n}\\
z_{n+1} = z_0 - \sum_{n=1}^{n}\frac{d}{2^n}\\
where
\begin{cases}
d = +1, & \text{if $z_n$>0} \\
d = -1, & \text{if $z_n$≤0}
\end{cases}
x n + 1 = x n = x 0 y n + 1 = y 0 + n = 0 ∑ n 2 n d x n z n + 1 = z 0 − n = 1 ∑ n 2 n d w h e r e { d = + 1 , d = − 1 , if z n >0 if z n ≤0
双曲坐标系
双曲坐标系的cordic旋转比较类似于圆周坐标系。
注意特殊的重复迭代 。
应用问题 cordic功能表 图源为参考文献[6] ,侵删。
cordic计算范围及转换
cordic算法的计算是有范围限制的,超范围的值需要进行转换后才能利用cordic算法进行计算。
cordic计算误差
近似误差和舍入误差
见参考文献[7]
FPGA实现 总结 未完待续…长期施工中…
参考资料 [1] 邹熙. 基于CORDIC的指数函数的FPGA实现[J]. 大众科技, 2008, 000(010):36-37.
[2] 三角函数计算,Cordic 算法入门
[3] CORDIC_百度百科
[4] 周晓青, 李合生, 陶荣辉, et al. 基于CORDIC算法的双曲正余弦函数FPGA实现[J]. 太赫兹科学与电子信息学报, 2010(2):211-214.
[5] cordic算法详解 转载
[6] Xilinx CORDIC算法
[7] Y. H. Hu, “The Quantization Effects of the CORDIC Algorithm”, in IEEE Trans. On Signal Processing, Vol 40,